Uma barcaça tem de largura e de comprimento e flutua com um calado de . Ela recebe uma carga de cascalho tal que seu centro de gravidade está acima da linha d’água. Ela é estável?
Passo 1
Que termos são esses? Barcaça, calado, cascalho? Hein?
Relaxa que o dicionário Auré..., digo, Responde Aí, vai te ajudar 😉 Primeiro, vamos visualizar o que está acontecendo com essa barcaça, que é uma barca grande (sim! é isso mesmo, rs)
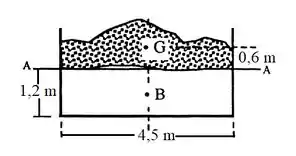
A barcaça é essa “caixa” da figura. Ela tem 4,5 m de largura e o comprimento de 12 m está entrando no papel.
E o que significa calado? Calado é a profundidade do fundo da barcaça até onde o fluido deixa de tocar a embarcação, ou seja, é a medida do fundo até o que chamamos de linha d’água. Essa linha está representada pela letra A na figura.
Essa barcaça está transportando um monte de lascas de pedras, que é a carga de cascalho, representadas na figura pela parte cheia de pontos. O enunciado diz que o centro de gravidade (G) dessa barcaça carregando cascalho está 0,6 m acima da linha d’água. Ou seja:
Ok! Agora que visualizamos o problema, vamos ver se essa barcaça está estável e de boa para transportar os cascalhos. Eles vão fazer diferença 😉
Passo 2
Como vimos na teoria, a barcaça com cascalhos vai ser estável se GM for maior que zero. Para calcular GM, usamos essa equação:
já conhecemos, então vamos calcular e depois .
O ponto de aplicação do empuxo fica na metade do volume submerso. Sabemos que a profundidade submersa (o tal do calado) é . Então:
Passo 3
Para calcular o , usamos a equação:
O momento de inércia da barcaça é o momento de inércia do retângulo na linha d’água
Onde Y é comprimento da barcaça (12 m) e X é a largura (4,5 m). Substituindo:
Para encontrar BM, precisamos saber o volume submerso:
Então:
Passo 4
Uhul! Hora de encontrar !
GM é maior que zero, logo, a barcaça transporta o cascalho de forma estável!
Resposta
Sim! Ela é estável. 😊