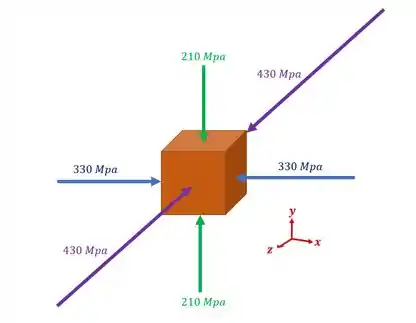
Uma barra de madeira será submetida a um carregamento triaxial que pode causar o seu rompimento. Sabendo que em um determinado momento foi analisado o seguinte elemento 3D retirado da barra no momento em que a mesma foi submetida ao carregamento. Sabendo que a barra possui e , determine se a barra suportaria ou não o carregamento assinalado.
Passo 1
Aqui podemos ver que se trata de um exercício sobre estado triaxial de tensões. Como não há tensões cisalhantes em nenhum dos planos, sabemos que esses planos já representam planos principais.
Mas aqui temos que lembrar o seguinte
Passo 2
Agora que já sabemos quais são as tensões principais, e também sabemos que o nosso elemento por não ter cisalhante também só possui tensões principais, basta relacionar todas as tensões.
Dessa forma teremos que
Já com esses valores podemos marcar os pontos de tensões principais
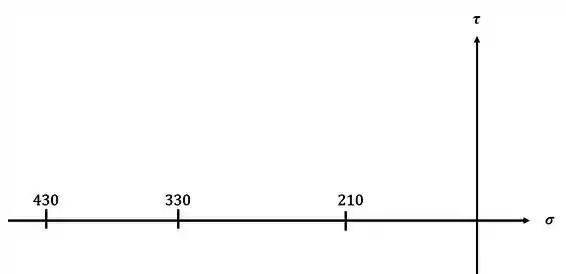
Já com isso em mãos basta apenas desenhar os círculos de Mohr
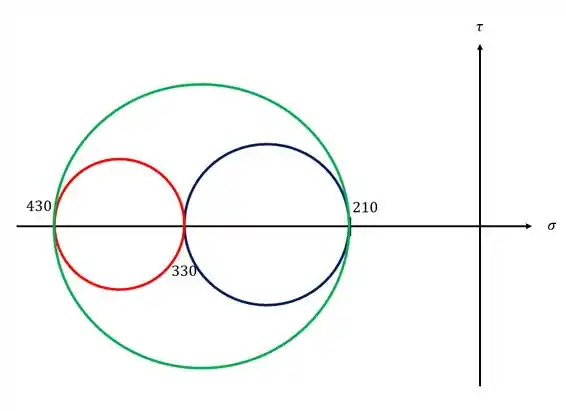
Passo 3
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por
Agora vamos pegar a resistência do nosso material, sabemos que
Sabemos que a nossa tensão máxima é
Que é menor que a nossa tensão admissível, ou seja, não ocorre rompimento da peça pelo efeito da tensão Normal.
Também sabemos que
Que apesar de estar próximo da nossa tensão admissível, não a ultrapassa, logo a nossa peça também está segura com relação a tensão cisalhante.
Resposta
Não ocorre rompimento da peça pois