Dado o elemento mostrado abaixo, determine as tensões normais e cisalhantes absolutas.
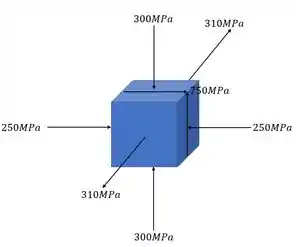
Passo 1
Podemos ver que se trata de uma questão em que o nosso elemento possui tensões cisalhantes em suas faces.
Quando há tensões cisalhantes, não podemos considerar os planos com essas tensões como planos principais.
O que sabemos é que o plano sem tensão cisalhante de fato representa um plano principal, mas nesse caso como não sabemos qual o valor dos outros dois planos só podemos afirmar isso até esse momento, ou seja,
Passo 2
Já sabemos que um dos planos se trata de um plano principal, mas como fazemos os outros dois também serem?
Basta usarmos os conceitos aprendidos na aula de transformação de tensões.
Basta analisar o seguinte elemento infinitesimal dado pelos esforços que agem nos planos com cisalhante.
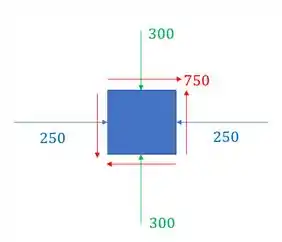
Agora é só determinar as tensões principais presentes nesse elemento infinitesimal.
Passo 3
Sabemos que para determinarmos as tensões principais precisamos usar
Que nos fornece a média das tensões
Que nós dá o cisalhante máximo que o nosso elemento foi submetido
A última fórmula é dada por
Que de fato nos fornece o valor das tensões principais
Sabemos que
Substituindo teremos que
Organizando teremos que
Passo 4
Agora vamos desenhar os círculos de Mohr para as nossas tensões
Primeiro vamos marcar os pontos
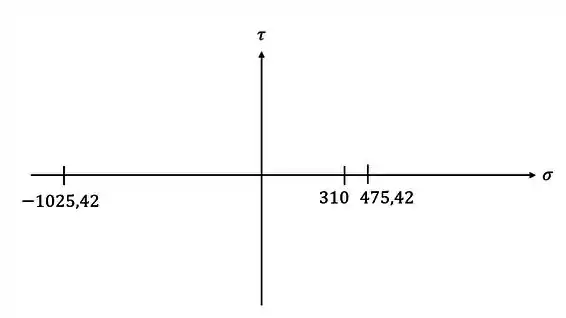
Agora vamos desenhar os círculos de Mohr
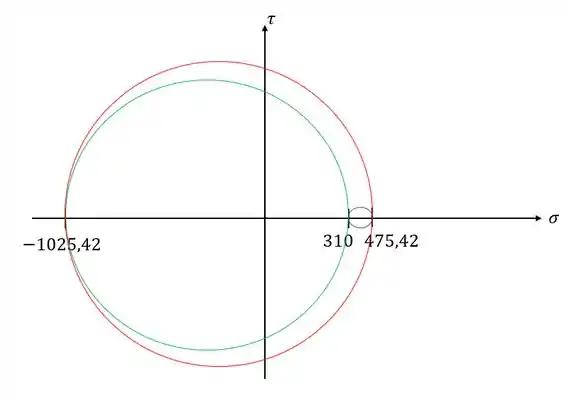
Agora fica fácil definir as tensões absolutas
A tensão absoluta normal maior será
A tensão absoluta normal menor será
E a tensão absoluta cisalhante será dada por