A fossa das Marianas é o local mais profundo dos oceanos, atingindo uma profundidade de 11034m. Considere que um submarino é feito de um material com resistência ao cisalhamento de e resistência ao normal de . Sabendo que a pressão de água é calculada pela fórmula P=dgh e que essa pressão age igualmente em todas a direções do nosso elemento tridimensional. A água não oferece resistência cisalhante. Nas direções x e z surgem acréscimos de tensões de -100Mpa e 85Mpa respectivamente, devido a tensões internas causadas pela idade do submarino. Sabendo disso, determine se o material constituinte desse submarino suportaria chegar ao fundo da fossa das Marianas.
Passo 1
Primeiro devemos desenhar o nosso elemento tridimensional e acrescentar as tensões presentes no nosso elemento.
Primeiro colocar a pressão devido a ação da água.
O valor dessa pressão é calculado por
Logo, em cada face haverá ação de 110Mpa comprimindo, agora vamos acrescentar as tensões ditas no enunciado na direção x e z.
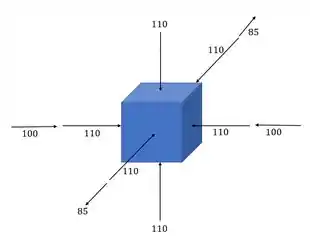
Somando as tensões na mesma direção teremos que
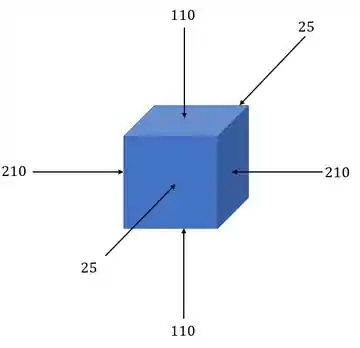
Passo 2
Agora que já sabemos quais são as tensões principais, e também sabemos que o nosso elemento por não ter cisalhante também só possui tensões principais, basta relacionar todas as tensões.
Dessa forma teremos que
Desenhando os círculos de Mohr
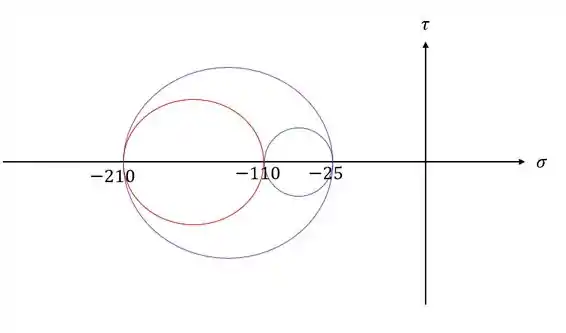
Passo 3
Agora vamos analisar a resistência ao normal, sabemos que
Como a resistência da nossa peça ao esforço normal é de 300Mpa, sabemos que o material chegara ao fundo da fossa das marianas sem romper pelos esforços normais.
Agora analisando o cisalhante teremos que
Como a resistência ao cisalhamento da nossa peça é de 90 Mpa, sabemos que o material do nosso submarino rompera pelo esforço cisalhante.
Resposta
Pelos cálculos vimos que o submarino não chagará ao fundo da fossa das marianas pois acabaria tendo o seu material constituinte rompendo pela ação do esforço cisalhante máximo de 92,5 Mpa.