A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Passo 1
O que está acontecendo?
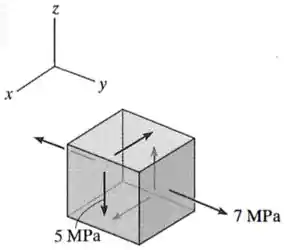
Nesse exercício, nós temos um elemento 3D de tensões em que existe:
- Uma tensão de cisalhamento no plano , que é negativa por não estar apontando para o primeiro quadrante entre os eixos e ;
- E uma tensão normal no eixo , que é positiva por ser de tração.
Aí, para esse elemento, como não existe nenhuma tensão de cisalhamento ou envolvendo o eixo , podemos concluir que o eixo já está livre de cisalhamento.
Isso significa que a tensão no eixo já é então uma das tensões principais desse elemento. (Só não sabemos qual...)
E o que é que o exercício quer?
Ele quer que a gente determine as tensões principais , e para esse elemento, além da tensão de cisalhamento máxima absoluta para ele:
Nós já conhecemos uma das tensões principais: a tensão de que ocorre no eixo , livre de cisalhamento.
Então para determinar as outras duas tensões principais, nós podemos esquecer do eixo e focar no que resta, que é o plano :
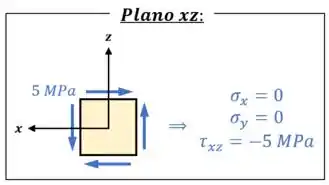
Calculando a tensão normal média para esse plano e fazendo o círculo de Mohr para ele, vamos conseguir calcular o raio desse círculo, para, em seguida, determinarmos as suas tensões principais:
Aí, com essas duas tensões principais do plano , mais a tensão principal do eixo , vamos conseguir:
- Desenhar os três círculos de Mohr para esse estado triaxial de tensões;
- Ordenar as tensões principais encontradas, definindo assim as tensões principais , e ;
- E calcular a tensão de cisalhamento máxima absoluta nesse ponto, .
Passo 2
Então vamos começar fazendo o círculo de Mohr do plano .
Lembra aí!
Para fazer isso, precisamos calcular para esse plano:
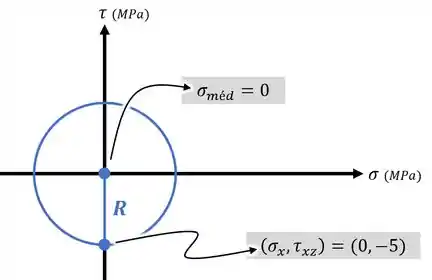
Feito isso, podemos marcar esse ponto e o ponto em um gráfico e usar esses pontos para desenhar o nosso círculo:
Passo 3
Agora, usando o círculo que acabamos de fazer, conseguimos identificar que:
E aí, podemos fazer que:
E substituir e para encontrarmos as tensões principais do plano :
Isso significa que o nosso elemento 3D, além da tensão principal de que já tínhamos identificado, ainda tem uma tensão principal de e outra de .
Passo 4
Agora que sabemos as três tensões principais do nosso elemento 3D, podemos complementar o círculo de Mohr que fizemos para o plano com elas.
Fazendo isso, vamos obter os três círculos de Mohr para o nosso elemento 3D e ao mesmo tempo identificar qual tensão principal é qual (, ou ):
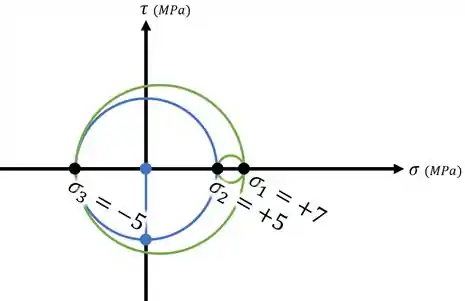
Se quisermos, ainda podemos identificar os círculos:
- O círculo interno à esquerda, entre as tensões principais e , descreve o que ocorre se a gente rotacionar o elemento em volta do “eixo 1” (aquele em que ocorre a tensão principal );
- O círculo externo, entre e , descreve a rotação em volta do “eixo 2”;
- E o círculo interno à direita, a rotação em volta do “eixo 3”:
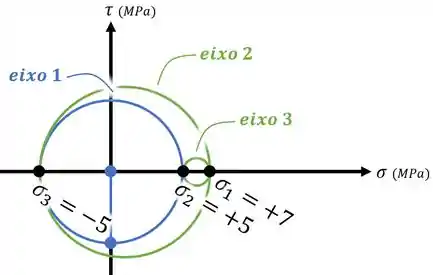
Passo 5
Por fim, podemos calcular a tensão de cisalhamento máxima absoluta nesse elemento fazendo:
Aí, substituindo e , vamos ter:
E pronto!
Está resolvido o nosso exercício.