Desenhe os três círculos de Mohr que descrevem cada um dos seguintes estados de tensão.
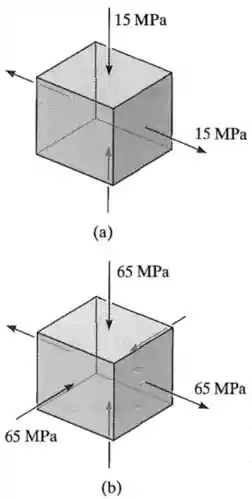
Passo 1
O que está acontecendo?
Tanto no item quanto no item , o exercício nos forneceu estados triaxiais de tensão em que não há nenhuma tensão de cisalhamento .
O que isso significa é que as tensões normais mostradas nesses elementos já são as tensões principais , e neles.
E o que é que o exercício quer?
Ele quer que a gente desenhe os três círculos de Mohr para cada um desses estados de tensão.
Então, o que devemos fazer para cada item é:
- Identificar e ordenar as tensões principais , e ;
- Marcar essas tensões em um gráfico ;
- & desenhar os três círculos entre esses pontos marcados.
Passo 2
Então vamos lá!
Começando pelo item :
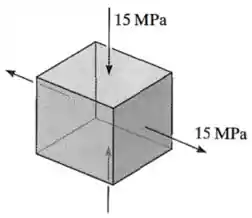
Nesse elemento, em uma direção nós temos uma tração de , em outra uma compressão de e em outra nenhuma tensão normal, ou seja, .
Sendo assim, vamos ter então tensões principais de , e .
Ordenando essas tensões, encontramos que:
Aí, marcando esses três pontos em um gráfico e desenhando círculos entre eles, obtemos a nossa resposta para o item , que é o desenho abaixo:
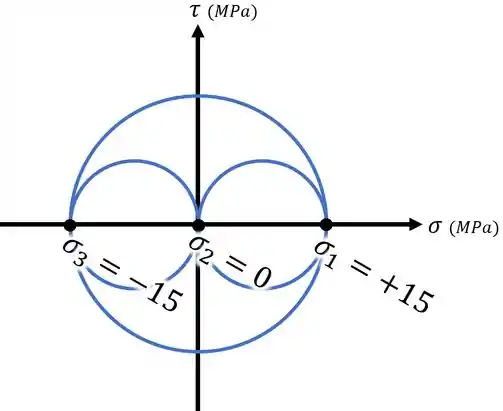
Passo 3
Já no item :
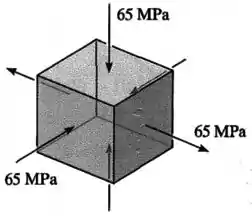
...nós temos em duas direções compressões de , e na outra direção uma tração de .
Dessa forma, nossas tensões principais vão ser de , e .
Ordenando essas tensões, encontramos que:
Aí, marcando esses três pontos em um gráfico e desenhando círculos entre eles, obtemos a nossa resposta para o item , que é o desenho abaixo:
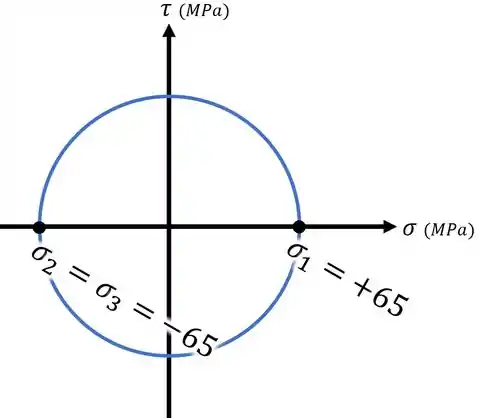
Observação:
Esse exemplo é interessante pois dá para ver nele como um dos círculos (o círculo formado entre e ) se reduziu a um ponto, fazendo com que os outros dois círculos fossem coincidentes.
E aí com isso, ficamos com essa situação em que aparentemente só temos 1 círculo de Mohr.