Encontre uma expressão analítica de uma transformação linear tal que a imagem de seja gerada pelos vetores e . A transformação linear encontrada é a única que satisfaz a condição dada no exercício?
Passo 1
Tá, ele quer uma transformação que vá do para o e que tenha como imagem o espaço gerado por e . Para “criarmos uma ” precisamos da aplicada em uma base do domínio. Mas ele não deu mais nenhuma condição pra gente, então vamos fazer o seguinte:
Agora vamos aplicar a nossa fórmula de bolo:
E pronto, temos uma com a imagem que o enunciado pediu.
Passo 2
Agora que montamos uma expressão para , será que ela é a única possível??
Não!! Fica fácil de ver, se lembrarmos do jeito que construímos a . Veja que tivemos que chutar uma base para o nosso domínio, porém poderíamos ter escolhido outros vetores para a base, que conseguiriam satisfazer as mesmas condições do exercício! Escolhemos esses pra facilitar nossa vida mesmo!
Passo 3
De fato, poderíamos ter respondido à segunda pergunta com o teorema da unicidade da transformação linear, que diz que é preciso ter uma base, e a imagem de cada um dos vetores da base, para a transformação ser única! Se não tiver as condições do teorema, a transformação não é única.
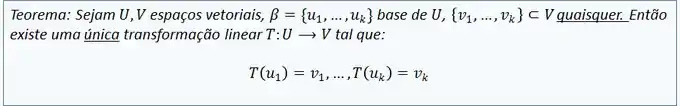
Resposta
Não.