Seja um espaço vetorial de dimensão finita com produto interno , e seja

um operador linear. Considere as seguintes afirmações:

1. Se o operador é simétrico então a matriz é simétrica, para qualquer base de
2. Se existe uma base ortogonal de formada pelos autovetores de , então o operador é simétrico
3. Se para todos , então o operador é simétrico

Quais afirmações são verdadeiras?

Queremos verificar se 3) é verdadeira. Isto é:

Se para todos ,então o operador é simétrico.

Para podermos verificar essa afirmação, precisamos relembrar a definição de operador simétrico e de uma propriedade do produto interno. Vamos lá!!!

Um operador é dito simétrico se

Isto é, se ele é igual ao seu transposto.

E temos a seguinte propriedade do produto interno:

Agora temos tudo que é preciso para verificar se 3) é verdadeira.

Usando as propriedades que revisamos no passo anterior, temos:

(mas temos como hipótese que )

(usando o fato que o produto interno é simétrico)

(juntando as equações temos)

(Usando a propriedade que revisamos)

Então

. Logo a afirmação 3) é verdadeira

Agora que verificamos a afirmação 3) vamos verificar a 2). Essa afirmação diz o seguinte:

Se existe uma base ortogonal de formada pelos autovetores de , então o operador

é simétrico.

Primeiro, vamos revisar o que é um operador ortogonal. é dito ortogonal se

Isto é, se sua inversa é sua transposta.

Essa afirmação fala de uma base ortogonal de formada com os autovetores de

isso lembra alguma coisa? O que vocês acham?

Exatamente diagonalização, temos uma base ortogonal de de autovetores de , então

é diagonalizável. Bacana né?

Sendo assim, nosso operador pode ser escrito como

, com diagonal.

Então:

(usando a associatividade do produto matricial)

(transposta do produto troca a ordem do produto e transpõe as partes)

(transposta do produto troca a ordem do produto e transpõe as partes)

(mas como P é ortogonal)

Ou seja,

é simétrica

Por fim, só resta verificar a primeira afirmação:

A afirmação 1) diz o seguinte: Se o operador é simétrico então a matriz é simétrica, para qualquer base de de

Essa é uma afirmação trabalhosa de verificar. Mas ficará tudo claro no nosso contra exemplo!!!

Nosso contra exemplo deve mostrar que uma transformação linear

simétrica pode ser expressa de forma não simétrica em alguma base

Considere a seguinte base e a matriz de transformação abaixo

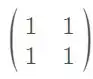
Então, nossa matriz

é:

Onde é o vetor representado na base . e é a matriz que leva da base canônica para a base e suas colunas são:

Vamos começar construindo a matriz .

Então nossa matriz

é:

Já estamos na metade do contra exemplo, ânimo!!!

No passo anterior calculamos . Agora só precisamos calcular para

(substituindo e1 pela sua representação na base beta)

(calculando o produto entre matriz vetor)

(substituindo e2 pela sua representaçãona base beta)

(calculando o produto entre matriz vetor )

Juntando esses resultados vemos que nossa matriz abaixo não é simétrica.

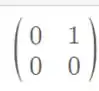
Logo a primeira afirmação é falsa!!!

E com isso chegamos ao fim de mais uma questão de algelin. Espero que os passos tenham ficado claros. Até a próxima!!! 😊