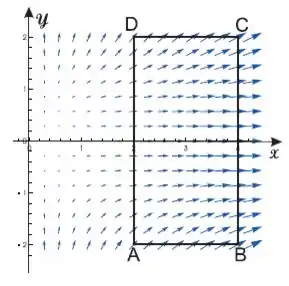
Considere um campo de vetores e uma curva , fechada, de forma retangular, como na figura abaixo. Analise o sinal da integral de linha ( é o versor normal exterior) sobre cada um dos segmentos de . O fluxo de sobre é positivo ou negativo? Justifique as respostas.
Passo 1
Essa questão é resolvida basicamente pelos conceitos de produto escalar. Nós queremos saber o sinal da integral de linha
Para cada um dos segmentos do retângulo. Vamos começar com o segmento .
Se a curva está orientada com a normal apontando para fora e, nesse trecho, o campo (como vemos pela figura) tem a mesma direção e sentido de , sabemos que o produto escalar é positivo.
Em outras palavras: a projeção do campo na direção de tem o mesmo sentido de , portanto, o fluxo é positivo.
Seguindo esse mesmo raciocínio para o trecho , temos o resultado oposto: o fluxo é negativo. Isso porque a projeção do campo na direção de tem sentido oposto a .
Passo 2
Em resumo: a orientação positiva de é com a normal para fora, logo, onde o campo “sai”, o fluxo é positivo, onde ele “entra” é negativo.
Em e é negativo e e positivo.
Passo 3
Agora vamos analisar o fluxo total em . Sabemos que em dois trechos o fluxo é positivo e em outros 2 negativo, mas isso não quer dizer que o total é zero!
Esses fluxos tem valores diferentes, dependendo do tamanho do vetor do campo no trecho.
Se você reparar, nos trechos e o campo tem o mesmo módulo, ou seja, seus vetores têm o mesmo tamanho. Portanto, os valores absolutos dos fluxos são o mesmo, porém, com sinal contrário. Assim, temos:
Passo 4
Agora vamos ver os trechos e . O primeiro tem fluxo negativo e o segundo, positivo, sendo que o campo tem módulo maior no segundo. Portanto, podemos escrever:
Passo 5
Sobre o fluxo total temos:
Logo, o fluxo total é positivo.