Use o Teorema de Green para encontrar a circulação no sentido anti-horário e o fluxo exterior para o campo e a curva : quadrado limitado por , , , .
Passo 1
Lembra como se calcula a circulação de um campo vetorial sobre uma curva C? Temos que usar essa integral de linha:
É útil desenhar a curva que foi descrita no enunciado:
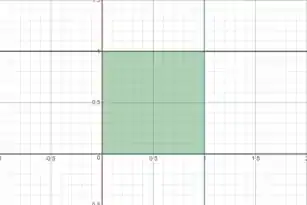
Quando calculamos a integral de linha do campo ao longo das bordas desse quadrado, o Teorema de Green permite que a gente diga o seguinte:
Como no nosso caso e , podemos usar o teorema para faciliar o cálculo da nossa integral de linha!
Beleza, então a integral que precisamos resolver para calcular a circulação é essa aqui:
Passo 2
Vamos começar calculando aquelas derivadas parciais:
Substituindo isso na integral:
Mas a gente sabe que é simplesmente a área da região definida pela curva ! Então se chamarmos essa área de , nossa integral é:
Como a região em questão é um quadrado de lado , a área é simplesmente:
E então:
Esse é o valor da circulação do campo pela curva !
Passo 3
Agora vamos ver o fluxo. Tome muito cuidado, porque aqui estamos trabalhando com o plano, e não com o espaço. Por isso, a definição do fluxo é essa aqui:
Parecida com a anterior né? Mas é bem diferente! Na circulação, nós integramos o produto escalar do campo com a tangente, aqui nos integramos o produto escalar do campo com a normal.
Mas tudo bem, isso foi só um esclarecimento, porque nós não vamos calcular essa integral diretamente, vamos usar o Teorema da Divergência (Gauss) no plano!
Lembra da fórmula nesse caso?
Onde esse é o divergente do campo vetorial .
Passo 4
Então vamos começar a resolver essa integral:
A fórmula para o é:
Onde , por exemplo, é a componente do campo vetorial . Então esse divergente vai ficar assim:
Substituindo isso na integral:
Passo 5
Como a região é quadrada (dê uma olhada na figura mais uma vez), é fácil definir os limites de integração:
Vamos resolver essa integral. Primeiro integrando em relação a . A integral indefinida é:
E então:
Agora vamos integrar em relação a . A integral indefinida é:
E então:
Pronto, esse é o valor da nossa integral, e portanto é o valor do fluxo do campo vetorial no interior da curva !
Resposta
A circulação vale e o fluxo vale .