Encontre o fluxo exterior do campo
Através do triângulo de vértices , , .
Passo 1
O que o exercício pede é o fluxo, que como vimos na teoria, podemos calcular por:
Mas a nossa curva é um triângulo, composto de 3 retas, de forma que:
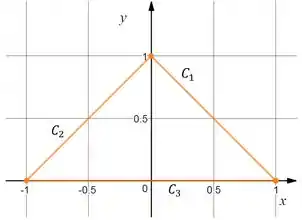
E por isso:
Então vamos calcular uma por uma pra ficar bem organizado!
Passo 2
Vamos começar por , que é a reta que vai de a , parametrizada por:
Lembramos que para encontrar o vetor normal, fazemos:
E jogamos na integral:
Até agora tudo bem, vamos ver a próxima!
Passo 3
Vamos repetir as contas, mas agora pra , que é a reta de a , com parametrização:
E o vetor normal a gente acha da mesma forma:
Então jogamos na integral de novo:
Só mais uma agora, vamos lá!
Passo 4
Pra fechar, temos que é a reta ligando a , que podemos parametrizar assim:
De novo, vamos ter o vetor normal:
E é só jogar na integral:
Pronto, agora é só somar tudo pra termos o resultado final!
Passo 5
Lembrando que gente tinha:
Então o fluxo exterior ao triângulo vai ser:
Nada tão bizarro assim, só um pouquinho trabalhoso, né? Mas agora já foi, o que importa é que resolvemos a questão. haha