Uma barra fina e homogênea de , com de comprimento, é dobrada em um semicírculo. Qual é a força gravitacional exercida pela barra sobre uma massa pontual de localizada no centro de curvatura do arco circular?
Passo 1
Vamos desenhar como vai ficar esse semicírculo:
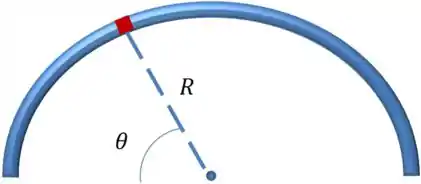
Agora, dá uma olhada nessa barra como um corpo extenso. Cada elemento de massa infinitesimal vai gerar uma força gravitacional infinitesimal na partícula:
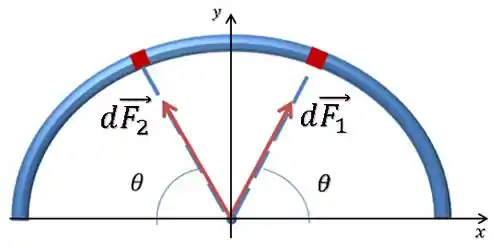
Além disso, temos uma simetria no nosso problema. Isso é um ótimo sinal, já que costuma simplificar nossas contas.
Podemos escrever em suas componentes:
E temos que seus módulos serão:
Você já deve estar pensando... que saco ter que calcular cada um desses termos.

Mas aí que a simetria entra em ação para nos ajudar.
Para cada ângulo na nossa figura, vamos ter uma componente apontando para o lado direito e uma componente , de mesmo módulo, apontando para o lado esquerdo.
Logo, elas vão se cancelar, sobrando apenas a componente em para cima:
Passo 2
Agora que temos uma expressão para a força exercida por cada elemento da barra, basta fazer um somatório de todas essas contribuições, ou seja, integrar:
A expressão da força gravitacional é:
No lugar de , chamamos de cada elemento infinitesimal de massa na barra, vamos chamar de a massa da partícula e, por último, temos que a distância entre os dois é sempre . Então:
Retirando as constantes da integral, temos:
Passo 3
Vamos achar algumas relações que nos permitem calcular a integral.
A densidade linear de massa continua a mesma, certo? Então:
Além disso, a densidade linear se relaciona com , da seguinte forma:
Temos também que a nossa barra é um arco de circunferência.
Podemos relacionar arcos e ângulos com:
Sendo o raio da circunferência e o ângulo percorrido pelo arco.
Com isso, podemos descobrir o valor do raio da barra :
Conseguimos também escrever o nosso assim:
Juntando isso tudo, temos que:
Passo 4
Agora, finalmente podemos calcular a integral.

Vamos substituir , lembrando dos limites de integração de que varrem de a , ou seja, de a :
Arrumando a casa:
Vamos resolver essa integral, rapidamente:
Chegamos, então, que:
Substituindo os valores, temos:
Para finalizar, resta lembrar que a direção do vetor força gravitacional resultante é em para cima.