Uma esfera homogênea de massa está localizada próximo a uma barra fina e homogênea de massa e comprimento , como na Figura 11-31. Determine a força gravitacional de atração exercida pela esfera sobre a barra.
Passo 1
Começamos aqui usando a simetria da esfera para acumular toda a sua massa em seu centro, criando forças que variam somente com o inverso do quadrado da distância.
Se liga na imagem:
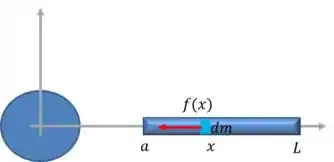
A expressão para será:
Como a barra é homogênea:
E a relação entre e é dada por:
Passo 2
Então, para encontrarmos a força total, basta integrarmos:
Logo:
Sabemos a direção e o sentido da força:
Resposta
Exercícios de Livros Relacionados
Um fio homogêneo de massa M tem a forma de um anel circular de raio a . Calcule a força de atração gravitacional exercida pelo fio sobre uma partícula de massa m situada sobre o eixo (perpendicular ao
Um furo é feito da superfície da Terra até o seu centro, como na figura 11-30. Ignore a rotação da terra e a resistência do ar, e trate a Terra como uma esfera homogênea. (a) Qual é o trabalho necessá
Na Fig. 13-39, uma partícula de massa m 1 = 0,67 k g está a uma distância de 23 cm de uma das extremidades de uma barra homogênea de comprimento L = 3,0 m e massa M = 5,0 k g . Qual é o módulo da forç
Determine a energia potencial gravitacional da barra fina do Exemplo 11-8 e de uma partícula pontual de massa m 0 que está no eixo x em x = x 0 , onde x 0 ≥ 1 2 L . (a) Mostre que a energia potencial
Considere um fio retilíneo homogêneo de massa M e comprimento L e uma partícula de massa m alinhada com o fio, à distância D de uma extremidade. Mostre que a força de atração gravitacional exercida pe