Determine a magnitude do campo gravitacional a uma distância de uma barra fina e homogênea de comprimento infinito, cuja massa por unidade de comprimento é .
Passo 1
Vamos desenhar o problema usando inicialmente uma barra de tamanho , depois de encontrar a expressão, a gente tende o pra infinito, beleza?
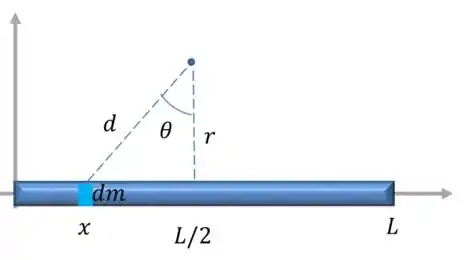
Como vamos integrar caminhando pelo eixo , precisamos de uma relação entre os infinitesimais de massa e de posição. Como a massa é homogênea e nos foi dado a densidade linear:
Passo 2
Essa massa vai exercer um campo no nosso ponto que está a uma distância da barra
Onde é o unitário apontando na direção de para o ponto em que estamos interessados.
Passo 3
Para cada pedaço da barra a esquerda do nosso ponto vamos ter um pedaço a direita. Se somarmos a contribuição de campo que cada pedaço faz vamos ter um campo na direção vertical como na figura abaixo!
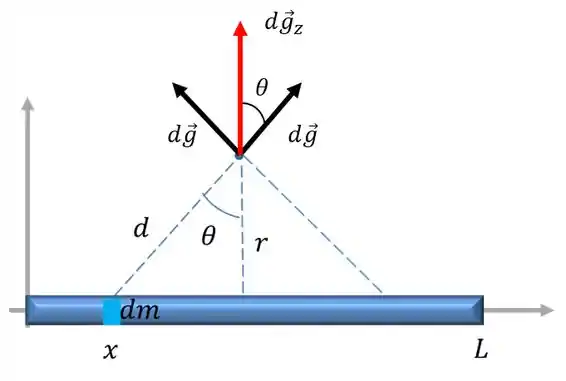
Assim o nosso campo resultante aponta na direção ! Então para pegar a componente temos que multiplicar o nosso campo por
Passo 4
Pela figura conseguimos ver um triângulo retângulo com catetos e e hipotenusa , assim
E também conseguimos calcular o cosseno de
Juntando tudo isso finalmente temos
Agora só falta integrar esse troço!
Passo 5
Sabemos que, para encontrar a magnitude do campo integral total da barra, vamos integrar o campo gerado por cada caquinho de massa:
Essa integral fica mamão com açúcar fazendo a substituição
Quando , temos que e quando , temos que
Derivando dos dois lados, temos
Substituindo o lá na integral, e mudando o intervalo de integração
Vamos focar nessa integral aqui
Lá embaixo no denominador, vamos colocar o em evidência
Aí agora a gente tem que usar aquela relação trigonométrica SUPER ÓBVIA (#sqn)
Aí a nossa integralzinha fica
Lembra o que é secante?!?!? É isso aqui ó
De forma que aquela integral monstra vira isso
Agora eu faço até com os pés nas costas!
Assim (FINALMENTE)
E voltando pro nosso campo
Como o enunciado pede a magnitude