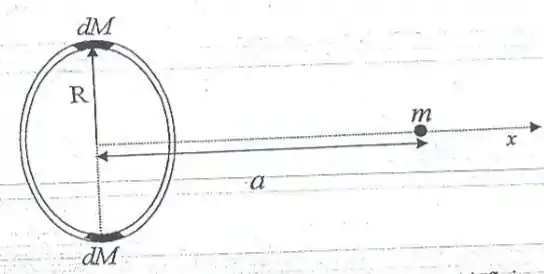
A figura abaixo representa um anel delgado de raio e massa homogênea e uma massa pontual que está situada no eixo que passa pelo centro do anel a uma distância do mesmo. Dois elementos infinitesimais de massa do anel, diametralmente opostos, são ilustrados na figura.
(a) Calcule o módulo da força resultante gravitacional infinitesimal que atua sobre a massa pontual devido à presença das massas infinitesimais .
(b) Qual é o módulo da força gravitacional resultante sofrida pela massa pontual devido, agora, à presença de todo o anel?
(c) Obtenha o módulo da força gravitacional para e para .
Passo 1
(a)
Pela lei de Newton da Gravitação Universal cada massa exercerá uma força
As componentes das forças se somam e as demais se cancelam. Então:
Passo 2
(b)
Como o anel é homogêneo:
Onde é o comprimento de arco da massa . Assim, substituindo na equação do item anterior, temos:
Passo 3
(c)
Já temos o módulo de . Basta substituir o valor da distância até o centro do anel.
Para , temos que .
E para , vamos ter
Resposta
a)
b)
c)