Questão 2P1-2010
A figura abaixo representa um semicírculo delgado de raio e massa homogênea e uma massa pontual que está situada centro do semicírculo. Dois elementos infinitesimais de massa , situados em ponto, para qual o raio forma um ângulo em relação ao eixo- que passa pelo centro do semicírculo, com ilustrado na figura:
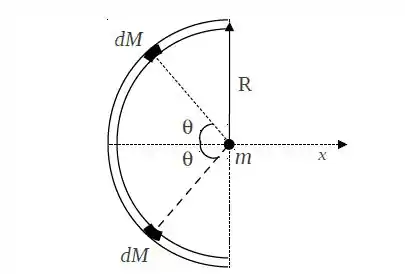
- Calcule o módulo da força gravitacional resultante que atua sobre a massa pontual devido à presença das massas infinitesimais
- Qual é o módulo da força gravitacional sofrida pela massa pontual devido, agora, à presença de todo o semicírculo.
- Usando o resultado do item b, obtenha qual seria a força sofrida pela massa no centro de um círculo completo.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Um fio homogêneo de massa M tem a forma de um anel circular de raio a . Calcule a força de atração gravitacional exercida pelo fio sobre uma partícula de massa m situada sobre o eixo (perpendicular ao
Um furo é feito da superfície da Terra até o seu centro, como na figura 11-30. Ignore a rotação da terra e a resistência do ar, e trate a Terra como uma esfera homogênea. (a) Qual é o trabalho necessá
Na Fig. 13-39, uma partícula de massa m 1 = 0,67 k g está a uma distância de 23 cm de uma das extremidades de uma barra homogênea de comprimento L = 3,0 m e massa M = 5,0 k g . Qual é o módulo da forç
Determine a energia potencial gravitacional da barra fina do Exemplo 11-8 e de uma partícula pontual de massa m 0 que está no eixo x em x = x 0 , onde x 0 ≥ 1 2 L . (a) Mostre que a energia potencial
Considere um fio retilíneo homogêneo de massa M e comprimento L e uma partícula de massa m alinhada com o fio, à distância D de uma extremidade. Mostre que a força de atração gravitacional exercida pe