Escreva as possíveis formas canônicas de Jordan do operador cujo polinômio característico é e cujo polinômio minimal é .
Passo 1
Bom, de cara conseguimos reparar que os autovalores são 3 e 2, com multiplicidade 5 e 4, respectivamente.
Então, a matriz deve ter 5 entradas 3 e 4 entradas 2 na diagonal.
Além disso, ambos os autovalores são elevados a 2 no polinômio minimal. Então o bloco elementar de maior ordem de ambos os autovalores deve ter ordem 2.
Ficamos, então, com as seguintes possibilidades:
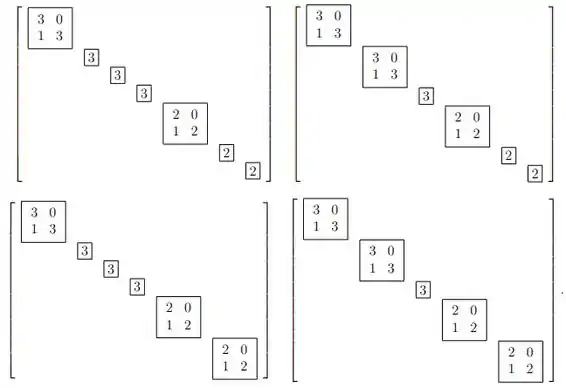
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Quais das seguintes matrizes estão na forma canônica de Jordan. a ) 2 1 0 0 0 0 2 0 0 0 0 0 - 1 1 0 0 0 0 - 1 0 0 0 0 0 - 1 b )2 1 0 0 0 0 0 2 1 0 0 0 0 0 2 1 0 0 0 0 0 2 0 0 0 0 0 0 2 0 0 0 0 0 0 - 1
Sejam C 1 , … , C k ciclos de autovetores generalizados associados a um autovalor λ . Mostre que se os vetores finais dos ciclos são distintos, então os ciclos são disjuntos, isto é, C i ∩ C j = ∅ , p
Seja T : V → V um operador tal que seu polinômio característico é da forma: p λ = - 1 n λ - λ 1 n 1 … λ - λ k n k , com λ 1 , … , λ k distintos. Seja w = L T - λ k m k . Mostre que:a) w é T-invariante
Seja T : V → V um operador tal que seu polinômio característico e da forma p λ = - 1 n λ - λ - 1n 1 … λ - λ k n k Com, λ 1 , … , λ k , distintos. Mostre que:(a) T é diagonalizável se, e somente se, o
Determine, se possível, uma matriz P , tal que P - 1 A P = J esteja na forma canônica de Jordan. c ) - 1 1 - 1 - 3 - 1 7 0 - 1 1 2 3 2 0 0 - 1 0 - 2 1 0 0 0 - 1 1 - 2 0 0 0 0 - 1 3 0 0 0 0 0 - 4