Encontre aproximações para usando polinômios interpoladores de Newton de graus , e usando os dados abaixo:
Passo 1
Montamos a tabela de diferenças divididas:
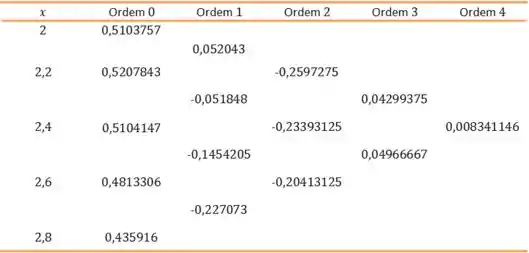
Passo 2
Um polinômio de grau requer valores . Como queremos uma aproximação em usamos:
E temos:
Nosso será:
Aproximando no nosso ponto de interesse:
Passo 3
Já um polinômio de grau requer valores . Então usamos:
E temos:
Nosso será:
Aproximando no nosso ponto de interesse:
Passo 4
E por último, um polinômio de grau requer valores . Então usamos:
E temos:
Nosso será:
Aproximando no nosso ponto de interesse:
Resposta
Exercícios de Livros Relacionados
Sabendo-se que a equação x - e - x = 0 admite uma raiz no intervalo (0, 1), determine o valor desta raiz usando interpolação quadrática. Estime o erro cometido, se possível. Justifique!
Consideremos o problema de interpolação para sen(x), numa tabela de pontos igualmente espaçados com intervalo h, usando um polinômio de 2º grau. Fazendo x 0 =- h ,x 1 = 0 ,x 2 = h , mostre que: | E (
14. Seja p n ( x ) o polinômio de grau ≤ n que interpola f ( x ) em x 0 , x 1 ,... x n escrito na forma de Newton.a) Escreva um algoritmo para avaliar p n ( x - ) , x - ∈ [ x 0 , x n ] semelhante ao a
9. Construa a tabela de diferenças divididas com os dadosa) Estime o valor de f ( 1.23 ) da melhor maneira possível, de forma que se possa estimar o erro cometido.b) Justifique o grau do polinômio que
Seja f ( x )=7 x 5 -3 x 2 -1 . a) Calcular f ( x ) nos pontos x=0 ;x = ± 1 ;x = ± 2 ;x = ± 3 (usar o algoritmo de Briot-Ruffini). Construir a seguir a tabela segundo os valores crescentes de x ; b) Co