Exercícios Resolvidos de Forma de Newton

Exercício 4 1 2 3 5 6 7 8

Enunciado

Seja tabelada e dada abaixo. Obter por interpolação linear.

Passo 1

A primeira coisa que a gente precisa fazer é construir a tabela de diferenças divididas, então partiu!!!

Como vamos fazer uma interpolação linear (usando uma reta), só precisamos das difereças de ordem 1.

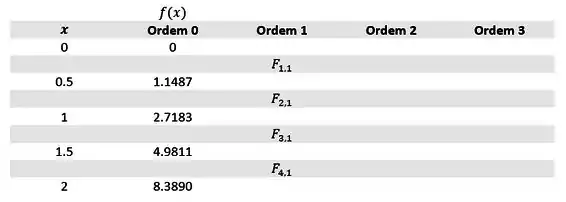
Bora achar esses para as difereças de ordem 1

Colocando na tabela de diferenças

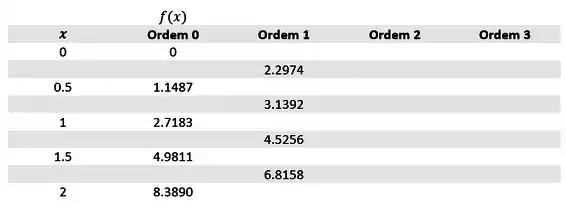
Como o professor nos pediu pra ajustar por uma reta, então basta ir até a ordem 1, nem precisa ir adiante não.

Passo 2

E agora josé?

Precisamos achar o , olhando pra tabela 0.7 tá dentro do intervalo [0.5,1]. Então vamo utilizar como e

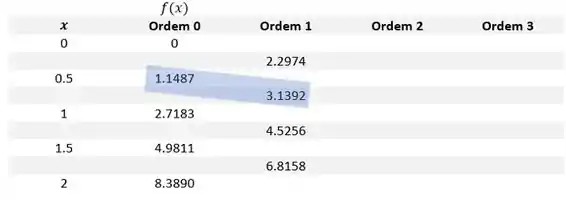
Nesse nosso exercício, já que ele é o primeiro valor tabelado do intervalo que a gente tá interessado.

Passo 3

Já que este polinômio aproxima a , a gente pode escrever o seguinte

Resposta

Exercícios de Livros Relacionados

Sabendo-se que a equação x - e - x = 0 admite uma raiz no intervalo (0, 1), determine o valor desta raiz usando interpolação quadrática. Estime o erro cometido, se possível. Justifique!

Consideremos o problema de interpolação para sen(x), numa tabela de pontos igualmente espaçados com intervalo h, usando um polinômio de 2º grau. Fazendo x 0 =- h ,x 1 = 0 ,x 2 = h , mostre que: | E (

14. Seja p n ( x ) o polinômio de grau ≤ n que interpola f ( x ) em x 0 , x 1 ,... x n escrito na forma de Newton.a) Escreva um algoritmo para avaliar p n ( x - ) , x - ∈ [ x 0 , x n ] semelhante ao a

9. Construa a tabela de diferenças divididas com os dadosa) Estime o valor de f ( 1.23 ) da melhor maneira possível, de forma que se possa estimar o erro cometido.b) Justifique o grau do polinômio que

Seja f ( x )=7 x 5 -3 x 2 -1 . a) Calcular f ( x ) nos pontos x=0 ;x = ± 1 ;x = ± 2 ;x = ± 3 (usar o algoritmo de Briot-Ruffini). Construir a seguir a tabela segundo os valores crescentes de x ; b) Co