Determine a tensão cisalhante máxima na seção sujeita ao esforço cortante mostrado abaixo. Todas as medidas estão em cm.
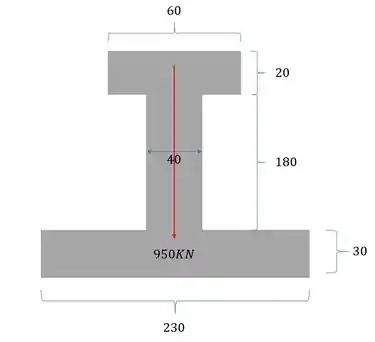
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata da altura em que alcançamos o cisalhante admissível da nossa peça, que também já sabemos ser 80Mpa).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
Precisamos determinar primeiramente a linha neutra na nossa seção. Sabemos que para determinarmos a linha neutra precisamos primeiro definir uma linha de origem, que geralmente passamos pela base da nossa seção.

Em seguida dividimos a nossa seção em figuras mais simples

Agora vem a parte legal, para cada uma dessas seções mais simples calculamos o valor da área e a distancia do centroide de cada uma delas até a nossa linha de origem.
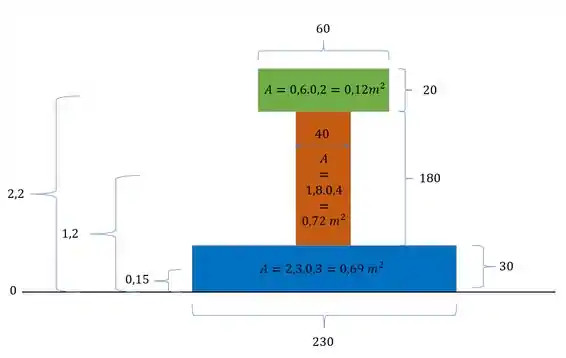
Agora para determinar a linha neutra basta usar a fórmula
Teremos que a linha neutra será marcada com relação a nossa origem
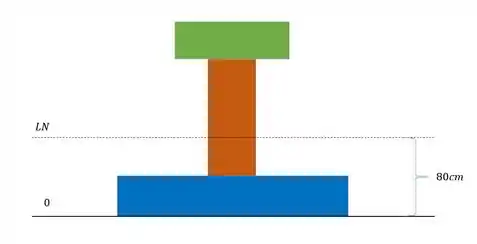
Sabemos também que o nosso cortante é dado no enunciado e sabemos que vale
Passo 3
Precisamos definir agora o valor do nosso momento de inércia. Aqui devemos seguir um passo a passo como seguimos para determinação da linha neutra.
Vamos utilizar a mesma separação de figuras mais simples que usamos para determinação da linha neutra

Já sabemos quanto valem as áreas de cada seção, mas agora devemos calcular dois valores importantes. Primeiro o momento de inercia de cada uma das peças mais simples. Depois a distancia do centroide de cada peça até a linha neutra. Na figura abaixo já verificamos tanto as áreas quando as distâncias dos centroides até a linha neutra.
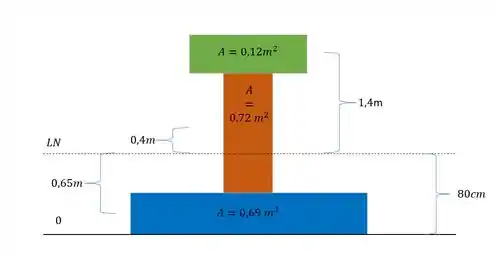
Vamos agora determinar o valor do momento de inercia para cada uma das peças. Sabemos que como todas são retângulos, a fórmula será
Olhando novamente as medidas teremos que
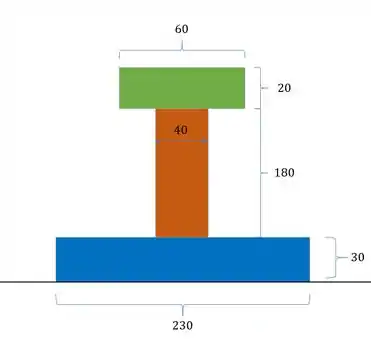
Logo
Com todos esses valores devemos usar a seguinte fórmula para determinarmos o momento de inercia da nossa seção
Substituindo nossos valores teremos que
Passo 4
Agora vamos determinar o momento estático da nossa seção. Como no enunciado foi pedido o valor do cisalhante máximo, devemos fazer o calculo levando em consideração as fibras da seção que contem a linha neutra, nesse caso a seção que usamos a cor laranja, dessa forma também descobrimos que o valor da espessura de fibras usada no nosso cálculo será
Mas também queremos determinar o momento estático, nesse caso devemos escolher a seção acima da linha neutra ou abaixo da linha neutra. Analisando a nossa seção, me parece mais simples fazer a conta analisando a parte de baixo da nossa seção, nesse caso pela nossa figura a nossa seção analisada será
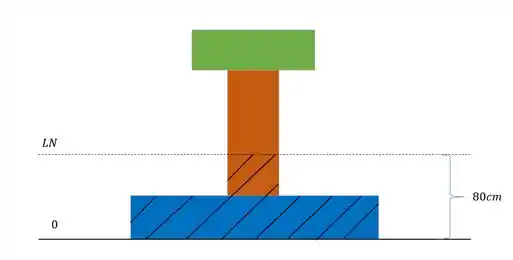
Podemos ver que essa região marcada em baixo possui duas seções diferentes, uma azul e uma laranja, dessa forma, para calcularmos o momento estático total precisaremos determinar o momento estático de cada um desses trechos e soma-los. Mas como calculamos o momento estático?
A fórmula é dada por
Em que é a área de cada seção abaixo da linha neutra e a distancia do centroide de cada seção abaixo da linha neutra até a própria linha neutra. No esquema abaixo descobrimos que esses valores são os da figura
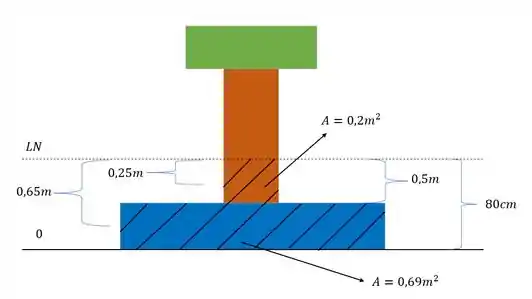
Agora basta substituir na fórmula os valores encontrados
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que