Se o tubo estiver sujeito a um cisalhamento , determine a tensão de cisalhamento máxima nele.
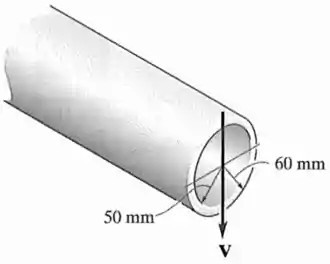
Dicas do Expert: Existem alguns conhecimentos adicionais importantes para resolver exercícios com uma seção circular como este.
São eles:
1. A tensão de cisalhamento máxima em seções transversais circulares (vazadas ou não) ocorre na linha neutra da seção;
2. Para o cálculo da posição da linha neutra, do momento de inércia da área e do momento estático, você pode considerar furos como elementos de área negativa e momento de inércia da área negativo;
& 3. A centroide de um semicírculo de raio fica a uma distância da base do semicírculo.
Passo 1
O que está acontecendo?
A seção transversal dessa viga tem a forma de um anel, com raio externo e raio interno .
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
Além disso, como essa seção é simétrica em relação à horizontal, já podemos afirmar que a sua linha neutra fica bem no seu meio:
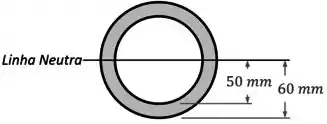
E o que é que o exercício quer?
Ele quer saber a tensão de cisalhamento máxima nessa seção, que vai ocorrer na sua linha neutra.
Então, devemos encontrar:
- O momento de inércia da área dessa seção;
- E o momento estático para a fibra na linha neutra.
Feito isso, vamos poder aplicar a fórmula do cisalhamento para a fibra na linha neutra “”, que vai ficar assim:
Sendo que a largura da seção nessa fibra vai ser igual ao diâmetro externo de menos o diâmetro interno de .
Ou seja, .
Passo 2
Então vamos começar calculando o momento de inércia da área para essa seção.
Para tanto, devemos separar ela em elementos individuais.
Nesse caso, podemos considerar o círculo maior como um elemento e o círculo menor, que é um furo, como um elemento de área negativa e momento negativo:
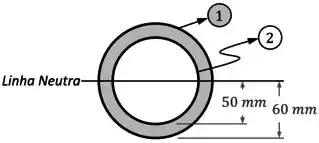
Como ambos os elementos são circulares, os seus momentos de inércia da área individuais vão ser dados pela fórmula:
Assim, para o elemento , de raio , vamos ter que:
Enquanto que para o elemento , de área/momento negativo e de raio , temos:
Aí, como os dois elementos já estão centrados na linha neutra, não é necessário utilizar o teorema dos eixos paralelos .
Ao invés disso, podemos simplesmente somar os momentos de cada elemento para encontrarmos o valor do momento de inércia da área da seção como um todo:
Passo 3
Em seguida, calculamos o momento estático para a fibra na linha neutra.
Para tanto, podemos escolher observar a região acima dessa fibra.
Fazendo isso, vamos ter dois elementos na forma de semicírculos.
O primeiro elemento, de raio , vai ter uma área positiva igual à metade da área de um círculo com esse raio:
E um centro com uma posição :
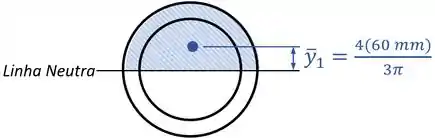
Já o segundo elemento, de raio , vai ter uma área negativa igual à metade da área de um círculo come esse raio:
E um centro com uma posição :
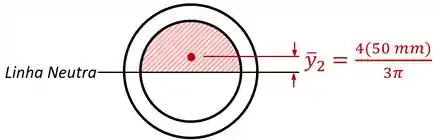
Dessa forma, o momento estático para a fibra na linha neutra vai ser:
O que dá:
Passo 4
Agora, só falta aplicar a fórmula do cisalhamento para o cálculo da tensão de cisalhamento máxima nessa seção, que ocorre na sua linha neutra.
Fazendo isso, temos:
Aí, substituindo:
- ;
- ;
- ;
- & ,
Vamos ter:
Calculando tudo e percebendo que o resultado final vai sair em , que é o mesmo que , encontramos que: