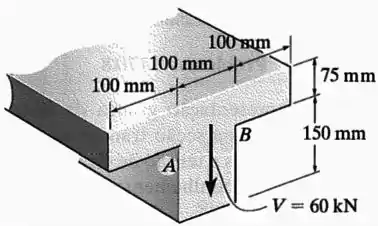
Se a viga for submetida a um cisalhamento vertical , determine a tensão de cisalhamento máxima na viga. Calcule também o salto da tensão de cisalhamento na junção aba-alma . Trace um rascunho da variação da intensidade da tensão de cisalhamento em toda a seção transversal.
Passo 1
O que está acontecendo?
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
E o que é que o exercício quer?
Ele quer saber:
- A tensão de cisalhamento máxima nessa seção;
- E o salto de tensão na junção aba-alma , que é a diferença entre a tensão nessa região para a aba de largura e a tensão nessa região para a alma de largura .
Para encontrar essas duas coisas, vamos ter que esboçar um gráfico para a distribuição da tensão nessa seção, que é a terceira coisa que o exercício pede.
Aí, para fazer isso, é só seguirmos os passos abaixo:
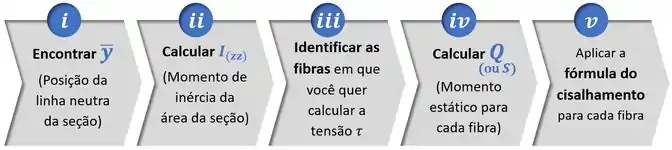
Então vamos lá!
Passo 2
Primeiro, precisamos determinar a posição da linha neutra dessa seção.
Para tanto, começamos separando a seção em elementos numerados e definindo uma posição na base da seção:
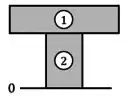
Em seguida, preenchemos em uma tabela os valores da área e da posição do centro de cada elemento:
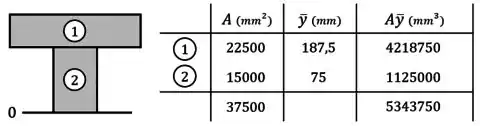
Ainda nessa tabela, também preenchemos na última coluna o produto desses valores para cada elemento e na última linha os somatórios e .
Com isso, podemos aplicar a fórmula:
E substituir os valores desses somatórios para encontrarmos a posição da nossa linha neutra:
Passo 3
Agora, já podemos calcular o momento de inércia da área da nossa seção como um todo.
Para tanto, devemos calcular, para cada elemento numerado:
- O momento de inércia da área ;
- E a distância do centro do elemento até a linha neutra.
(Não precisamos calcular as áreas pois já calculamos elas no passo anterior.)
Como os nossos dois elementos são retangulares, eles vão momentos de inércia da área .
Para o elemento , temos uma base e uma altura , então:
Já para o elemento , e , então:
Em seguida, como o elemento tem um centro a uma altura de e como a linha neutra está a uma altura de , a distância para o elemento vai ser:
Já o elemento tem um centro a uma altura de , de tal forma que:
Finalmente, podemos aplicar a fórmula:
Que fica assim para o nosso caso com dois elementos:
E substituir nessa fórmula:
- e ;
- e ; (Valores retirados da tabela do passo anterior)
- & e ,
Para encontrarmos que o momento de inércia da área da nossa seção como um todo é:
Passo 4
Próximo passo, identificar as fibras de interesse:
- As fibras no topo e na base da seção;
- As fibras onde ocorre uma mudança na largura da seção;
- E a fibra na linha neutra.
Fazendo isso, ficamos com o desenho abaixo:
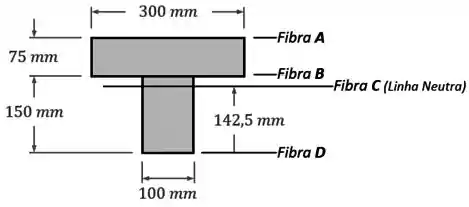
Sendo que nesse desenho, as dimensões foram adicionadas para já facilitar os cálculos do próximo passo.
Passo 5
Agora, devemos calcular os momentos estáticos .
Para as fibras e , podemos nos lembrar que os momentos estáticos das fibras no topo e na base de uma seção são iguais a zero, então:
Para a fibra , podemos escolher por observar a região acima dessa fibra.
Fazendo isso, vamos ter nessa região um único elemento retangular: o elemento que definimos anteriormente.
Esse elemento tem uma área e um centro com uma posição relativa à linha neutra .
Dessa forma, temos que:
Já para a fibra , é mais fácil escolher por observar a região abaixo desse fibra.
Nessa região, vamos ter um único elemento retangular encostado na linha neutra com uma altura de e uma largura de .
Dessa forma, esse elemento vai ter uma área e um centro com uma posição relativa à linha neutra .
Sendo assim, temos:
Passo 6
Finalmente, já temos tudo que precisamos para aplicar a fórmula do cisalhamento:
...para cada fibra.
Para as fibras e , como , vamos ter que:
Já para a fibra , temos:
Aí, como temos duas larguras na região da fibra ( e ), devemos aplicar essa fórmula duas vezes.
Primeiro, substituímos:
- ;
- ;
- ,
E a largura da aba, :
Calculando tudo, vamos ter um resultado final em , que é o mesmo que :
Em seguida, substituímos os mesmos valores, mas dessa vez utilizamos a largura da alma, :
Calculando tudo isso, encontramos que:
Por fim, para a fibra , temos:
Aí, substituindo:
- ;
- ;
- ;
- E a largura da seção na região da fibra , ,
Encontramos que:
Passo 7
Por fim, inserindo os valores de tensão encontrados no passo anterior em um gráfico, e conectando esses pontos sabendo que:
- A distribuição de tensões devido à força cortante é parabólica;
- E de que o ponto máximo dessas parábolas ocorre sempre na linha neutra da seção.
Ficamos com o gráfico abaixo, que faz parte da nossa resposta para o exercício:
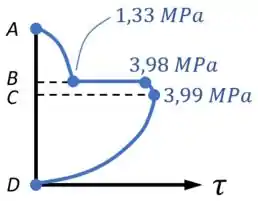
Além disso, desse gráfico...
Conseguimos identificar a tensão de cisalhamento máxima nessa seção e o valor do salto de tensão na junção aba-alma na fibra , que completam a nossa resposta para o exercício: