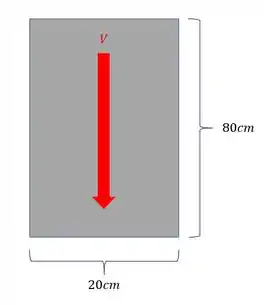
Uma viga de seção retangular com as dimensões mostradas na figura, foi submetida a um carregamento cortante de intensidade . Sabendo que a tensão cisalhante admissível máxima suportada por essa viga é , determine o valor do cortante máximo que podemos aplicar sem que haja rompimento da peça.
Passo 1
Para resolvermos essa questão precisamos analisar cada elemento da nossa fórmula a fim de descobrir em que ponto estará a nossa incógnita (que já sabemos de antemão que se trata do cortante).
A nossa fórmula para cisalhamento é dada por
Em que sabemos que
= tensão cisalhante
= esforço cortante
= Momento Estático
= Momento de Inércia
= espessura do ponto que calculamos o cisalhante
Agora que já sabemos o que cada termo da nossa fórmula significa, vamos identificar cada um desses valores na nossa seção.
Passo 2
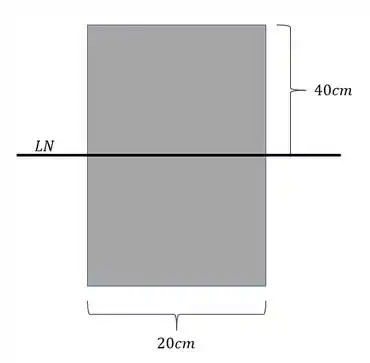
Precisamos determinar primeiramente a linha neutra na nossa seção. A linha neutra de uma seção retangular uniforme sempre fica no centro da nossa seção. Como queremos saber o máximo cortante que devemos aplicar precisamos usar o ponto que há o maior cisalhante na nossa peça, e nesse caso o ponto com maior tensão cisalhante é o ponto sobre a linha neutra.
Passo 3
Precisamos definir agora o valor do nosso momento de inércia. Como a nossa seção é retangular sabemos que o momento de inercia será
Em que
Passo 4
Agora vamos determinar o momento estático da nossa seção. Como no enunciado foi pedido o valor do cisalhante máximo, devemos fazer o cálculo levando em consideração as fibras da seção que contem a linha neutra, dessa forma também descobrimos que o valor da espessura de fibras usada no nosso cálculo será
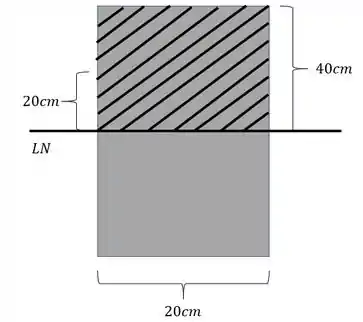
Mas também queremos determinar o momento estático, nesse caso devemos escolher a seção acima da linha neutra ou abaixo da linha neutra. Analisando a nossa seção, faremos isso para a seção acima da linha neutra como mostra a figura
A fórmula do momento estático é dada por
Em que
Com isso teremos que
Passo 5
Agora que já determinamos todos os valores basta substituirmos na nossa equação
Substituindo teremos que