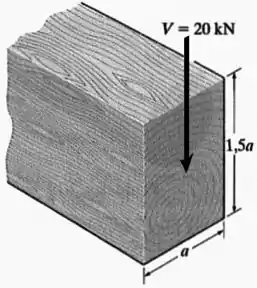
A viga tem seção transversal retangular e é feita de madeira com tensão de cisalhamento admissível . Se for submetida a um cisalhamento , determine a menor dimensão de sua parte inferior e de seus lados.
Passo 1
O que está acontecendo?
A seção transversal dessa viga é retangular, com uma base e uma altura .
Por causa da força cortante , vão surgir nessa seção tensões de cisalhamento de acordo com a fórmula do cisalhamento:
Onde:
- (também conhecido como “”) é o momento estático, calculado para uma fibra da seção;
- (também conhecido como ) é o momento de inércia da área da seção;
- & (também conhecido como ) é a largura da fibra em que se quer calcular a tensão .
Aí, como a seção dessa viga é só um retângulo, já sabemos que a sua linha neutra/centroide fica bem no meio da seção:
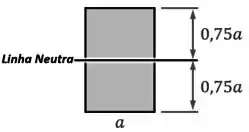
Além disso:
- O momento de inércia da área é sempre uma constante;
- E essa seção tem uma largura constante.
Então o que vai determinar aonde vai ocorrer a tensão máxima nessa seção é o momento estático .
E nós vimos na nossa teoria que o momento estático é sempre máximo na linha neutra:

Assim, concluímos que a tensão máxima nesse seção vai ocorre na sua linha neutra.
E o que é que o exercício quer?
Ele quer saber qual é o menor valor de necessário para que a tensão de cisalhamento máxima nessa viga não ultrapasse o seu valor admissível .
Ou seja, ele quer saber qual é o menor valor de que satisfaz a condição:
Então, para resolver esse exercício...
Devemos determinar o valor de para essa seção e depois determinar o valor do momento estático para a fibra na linha neutra.
Assim, vamos poder descrever a tensão nessa seção em função da dimensão .
Substituindo isso na condição acima, vamos poder isolar e encontrar seu valor mínimo necessário.
Passo 2
Então vamos começar pelo cálculo do momento de inércia da área para essa seção retangular.
Lembra aí!
O momento de inércia da área de um elemento retangular é dado pela fórmula:
Daí que, substituindo os valores:
- ;
- & ,
Encontramos que:
O que dá:
Beleza!
Passo 3
Em seguida, vamos determinar o valor do momento estático para a linha neutra, que é sempre o momento estático máximo em uma seção:
Agora lembra aí!
Para determinar o valor do momento estático, devemos:
- Observar somente a região acima OU abaixo da fibra;
- Separar a região escolhida em elementos individuais;
- Identificar, para cada elemento, a área e a posição do seu centro em relação à linha neutra da seção;
- E finalmente, aplicar a fórmula para a fibra em questão.
Fazendo isso para a fibra na linha neutra, e escolhendo observar a região acima dela, vamos ter um único elemento retangular, com a área e posição indicadas na imagem abaixo:
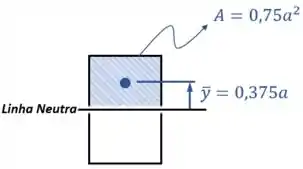
Dessa forma, vamos ter que:
O que significa que:
E pronto!
Passo 4
Agora, podemos pegar a nossa condição de projeto:
E aplicar a fórmula do cisalhamento com o objetivo de descrever a tensão máxima nessa seção.
Fazendo isso, a nossa condição fica assim:
Substituindo , e , vamos ter que:
Simplificando isso, temos:
Isolando :
Espelhando essa expressão e fazendo a raíz quadrada dos dois lados:
E substituindo:
- ;
- & ,
Encontramos que:
O que significa que o valor mínimo necessário para a dimensão é: