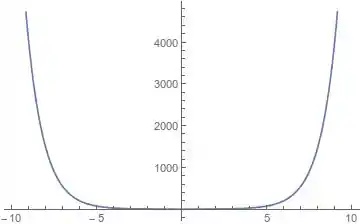
Esboce o gráfico de:
Passo 1
Não confunda essa expressão com identidade fundamental trigonométrica, lembre-se que:
Mas sim:
Vamos então tentar usar essa identidade para simplificar e então esboçá-lo. Para tal, vamos tentar escrever a expressão de maneira que a identidade fundamental apareça.
Se somarmos e subtrairmos dentro da raiz estaremos somando zero e, portanto, não alterando nada, certo? Então vamos fazer isso:
Agora vamos reorganizar para aparecer a identidade:
Olha ela lá! Vamos substituir:
Passo 2
Agora ficou tranquilo, né? Já vimos esse gráfico na teoria. A diferença é que, por aparecer o módulo, a parte positiva estará refletida para cima:
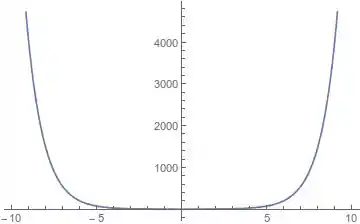
Resposta