Prove que
Passo 1
Para provarmos isso, vamos sair de um dos lados da igualdade e tentar chegar no outro... Por motivos lógicos, é muito mais fácil sairmos do lado esquerdo da igualdade e tentarmos chegar que isso é igual a 1. Vamos tentar?
Beleza, de início vamos trabalhar com as definições de Sendo assim, teremos:
Aplicando os produtos notáveis, teremos:
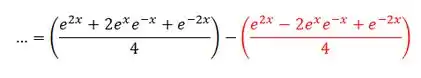
Reorganizando...
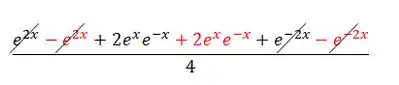
Lembrando que: , ficamos assim:
Como queríamos demonstrar.
Resposta
Ei, a resposta está no passo a passo :)