P3 de Álgebra Linear I - MAT1200 da PUCRIO - 2018.2

Seja Q uma matriz ortogonal

(a) Considere a matriz onde

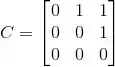
Determine explicitamente

(b) Determine os autovalores da matriz onde

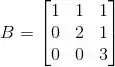
(a) Considere o produto interno em definido por

onde

Considere o subespaço vetorial de

Determine uma base do seu complemento ortogonal .

(b) Considere o subespaço vetorial

Encontre um produto interno em tal que o complemento ortogonal de seja

Considere a matriz

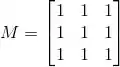
(a) Determine os autovalores de M.

(b) Determine uma base de autovetores de M.

(c) Diagonalize ortogonalmente M, ou seja, encontre matrizes P ortogonal e D diagonal tais que

Considere as bases de vetores e de onde

Considere a transformação linear definida por

Determine:

(a) A matriz de na base

(b) As matrizes de mudança de base da base para a base e da base para a base

(c) A matriz de na base

Considere agora o espaço vetorial dos polinômios de grau menor ou igual a 2 e suas bases

Podemos também usar a notação:

Considere a transformação linear que corresponde à derivada, definida por:

(d) Determine as matrizes de D na base e de na base