P2 de Álgebra Linear I - MAT1200 da PUCRIO - 2018.2

Considere os planos e de equações cartesianas

(b) Considere o conjunto de vetores

os vetores que estão escritos na base canônica. Mostre que é uma base de .

(c) Considere o vetor v cujas coordenadas na base são

Determine as coordenadas de v na base canônica.

Considere os planos e de equações cartesianas

(a) Determine uma base de e uma base de tais que as duas bases tenham um vetor comum.

Considere as transformações lineares A, B, C: cujas matrizes na base canônica são, respectivamente:

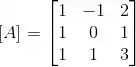
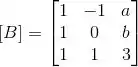
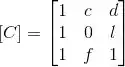
(a) Determine uma base do espaço imagem de A (ou, equivalentemente, o espaço coluna da matriz ).

(b) Determine a e b para que a imagem de B (ou, equivalentemente, o espaço coluna da matriz ) seja um plano.

(c) Determine c, d, l e f para que a imagem de C (ou, equivalentemente, o espaço coluna da matriz ) seja uma reta.

Considere a matriz

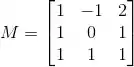
e a transformação linear cuja matriz na base canônica é M.

(b) Determine as coordenadas na base canônica do vetor v que verifica

Considere a matriz

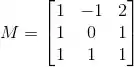
e a transformação linear cuja matriz na base canônica é M.

(a) Determine a matriz inversa de M.

Considere o plano de equação cartesiana:

e as transformações lineares P de projeção ortogonal no plano e E de espelhamento em relação ao plano .

(a) Determine a matriz de P na base canônica.

(b) Determine a matriz de E na base canônica.

(c) Determine a matriz da composição na base canônica.

(d) Encontre um plano (em equação cartesiana) tal que seja uma reta.