P4 de Álgebra Linear I - MAT1200 da PUCRIO - 2018.2

Considere as bases do

E a transformação linear cuja matriz na base é:

(c) Escreva, se possível, uma forma diagonal de T.

Considere as bases do

E a transformação linear cuja matriz na base é:

(a) Determine explicitamente as matrizes de mudança de base da base para a base e da base para a base

(b) Determine explicitamente a matriz da transformação linear T na base

Considere o plano em que passa pela origem de equação cartesiana

e a transformação linear espelhamento (ou reflexão) em relação ao plano Denote por a matriz de E na base canônica.

(d) Seja B uma matriz ortogonalmente diagonalizável. Mostre que Para isso lembre da forma

(e) Considere uma transformação linear que tem uma base ortonormal de autovetores e determinante 0. Seja:

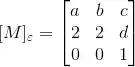
A matriz de M na base canônica. Determine os valores de a,b,c e d.

Considere o plano em que passa pela origem de equação cartesiana

e a transformação linear espelhamento (ou reflexão) em relação ao plano Denote por a matriz de E na base canônica.

(a) Considere a base ortonormal de

e o vetor (escrito na base canônica). Determine a segunda coordenada de v na base

(b) Escreva na forma , onde Q é uma matriz ortogonal e D é diagonal.

(c) Determine explicitamente a matriz

Considere a transformação linear definida por:

(a) Determine a matriz da transformação linear T na base canônica.

(b) Determine a equação cartesiana da imagem de T. Lembre que:

(c) Considere a base:

Determine a matriz da transformação linear T na base .

(d) Considere o plano de equação cartesiana:

Determine uma base da imagem de pela transformação T.