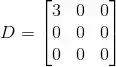Considere a matriz
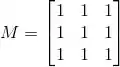
(a) Determine os autovalores de M.
(b) Determine uma base de autovetores de M.
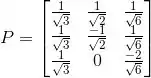
(c) Diagonalize ortogonalmente M, ou seja, encontre matrizes P ortogonal e D diagonal tais que
Passo 1
(a) Pra achar os autovalores da matriz, fazemos:
Então:
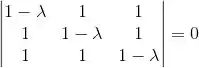
Ou seja, temos os autovalores:
Passo 2
(b) Para achar os autovetores de M, resolvemos o sistema linear:
para cada autovalor que encontramos no item (a).
Vamos começar com
Nesse caso, o sistema fica:

Sendo , temos uma única equação:
Então:
E os vetores vão ser:
Fazendo e , achamos o autovetor e fazendo e achamos o autovetor
Mas qualquer outra combinação linear entre esses dois caras também é autovetor, beleza?
Agora vamos resolver o sistema para :
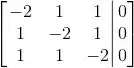
Escalonando:
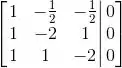
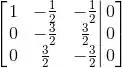
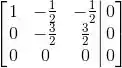
Sendo ficamos com um sistema com duas equações:
Da segunda equação, tiramos que:
Substituindo na primeira:
Então os vetores nesse caso vão ser:
Fixando , achamos um terceiro autovetor possível, que é
E de novo, qualquer múltiplo desse cara também é autovetor.
Então uma base de autovetores é dada por:
Passo 3
(c) Agora precisamos diagonalizar M ortogonalmente, ou seja, escrever M na forma:
onde P é uma matriz com autovetores ortonormais nas colunas e D é uma matriz diagonal com autovalores na diagonal principal.
Na letra (b), achamos uma base de autovetores:
Mas essa base não é uma base ortonormal (os autovetores não tem norma 1 e não são ortogonais dois a dois).
Bom, o autovetor é ortogonal aos autovetores e , mas esses dois últimos não são ortogonais entre si.
Vamos então manter os autovetores e na base e buscar um terceiro autovetor que seja ortogonal a esses dois.
Lembrem que para tínhamos encontrado que os autovetores eram:
Se fizermos e nessa combinação linear, obtemos:
E esse autovetor é ortogonal aos outros dois.
Então uma base ortogonal de autovetores é:
Pra fazer essa base ser ortonormal, basta dividir cada vetor pela sua norma:
Então temos as matrizes:
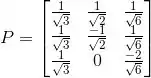
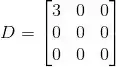
Resposta
(a)
(b)
(c)