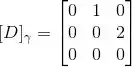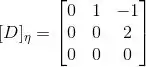Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Matriz de Mudança de Base

Ver Teoria
Exercício 24123456789101112131415161718192021222325262728293031323334353637383940

Enunciado

Considere as bases de vetores ε = { i , j , k } e β = v 1 , v 2 , v 3 de R 3 onde

i = 1,0 , 0 ,   j = 0,1 , 0 ,   k 0,0 , 1

v 1 = i = 1,0 , 0 ,   v 2 = i + j = 1,1 , 0 ,   v 3 = i + j + k = ( 1,1 , 1 )

Considere a transformação linear T : R 3 → R 3 definida por

T i = 0 = 0,0 , 0 ,   T j = i ,   T k = 2 j

Determine:

(a) A matriz T ε   de T na base ε .

(b) As matrizes de mudança de base da base ε para a base β e da base β para a base ε .

(c) A matriz T β de T   na base β .

Considere agora o espaço vetorial P 2 dos polinômios de grau menor ou igual a 2 e suas bases

γ = p i x = 1 , p j x = x , p k x = x 2

η = q 1 x = p i x , q 2 x = p i x + p j x ,   q 3 x = p i x + p j x + p k x

Podemos também usar a notação:

γ = 1 , x , x 2

η = 1,1 + x , 1 + x + x 2

Considere a transformação linear D : P 2 → P 2 que corresponde à derivada, definida por:

D p i x = D 1 = 0 ,   D p j x = D x = 1 , D p k x = D x 2 = 2 x

(d) Determine as matrizes D γ de D na base γ e D η de D   na base η .

Passo 1

(a) Para achar a matriz T ε   de T na base ε , precisamos da transformação T aplicada aos vetores da base ε .

A base ε   é a base canônica do R 3 :

ε = i , j , k = { 1,0 , 0 , 0,1 , 0 , 0,0 , 1 }

E o enunciado deu pra gente que:

T i = 0 = 0,0 , 0

T j = i = ( 1,0 , 0 )

T k = 2 j = ( 0,2 , 0 )

Como ε é a base canônica, basta colocar esses resultados da transformação nas colunas de uma matriz!

Logo:

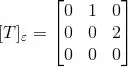
Passo 2

(b) Vamos começar achando a matriz de mudança de base da base ε para a base β , que vamos denotar por I d β ← ε .

Pra acha-la, precisamos escrever os vetores da base do domínio (que é a ε ) nas coordenadas da base β do contradomínio e depois colocar os resultados nas colunas de uma matriz, respeitando a ordem da base.

Temos:

1,0 , 0 β = 1 v 1

0,1 , 0 β = 1 v 2 - 1 v 1

0,0 , 1 β = 1 v 3 - 1 v 2

Então:

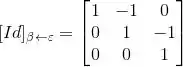
E agora, pra achar a matriz de mudança de base da base β   para a base ε vai ser a mesma coisa!

Vamos denotar essa matriz por I d ε ← β .

Pra acha-la, precisamos escrever os vetores da base do domínio (que agora é a β ) nas coordenadas da base ε do contradomínio e depois colocar os resultados nas colunas de uma matriz, respeitando a ordem da base.

Temos:

v 1 ε = 1 i

v 2 ε = 1 i + 1 j

v 3 ε = 1 i + 1 j + 1 k

Então:

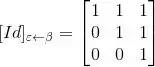
Passo 3

(c) Já que achamos as matrizes de mudança de base, vamos usá-las para achar a matriz T β de T   na base β :

T β = I d β ← ε T ε I d ε ← β

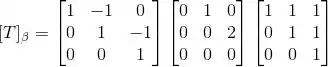
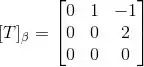
Passo 4

(d) De novo precisamos achar matriz que representa a TL, mas dessa vez os espaços vetoriais são espaços de polinômios.

Mas não se assusta porque é exatamente a mesma coisa que a gente viu antes!

Pra achar a matriz D γ de D na base γ , vamos aplicar a transformação D nos vetores da base γ e colocar os resultados nas colunas de uma matriz!

Lembra que só podemos fazer isso porque a base γ é a base canônica dos polinômios de P 2 ‼

Vamos lá, derivando os vetores da base γ :

D 1 = 0

D x = 1

D x 2 = 2 x

Então:

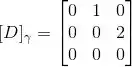
Agora pra achar a matriz D η de D na base η , vamos aplicar a transformação D nos vetores da base η e escrever os resultados em coordenadas da base η .

Depois a gente pega essas coordenadas e coloca nas colunas de uma matriz, respeitando a ordem da base!

Aplicando a transformação e escrevendo nas coordenadas da base η :

D 1 = 0 ⇒ 0 η = 0 1 + 0 1 + x + 0 ( 1 + x + x 2 )

D 1 + x = 1   ⇒ 1 η = 1 1 + 0 1 + x + 0 ( 1 + x + x 2 )

D 1 + x + x 2 = 1 + 2 x ⇒ 1 + 2 x η = - 1 1 + 2 1 + x + 0 ( 1 + x + x 2 )

Então:

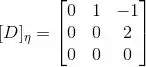
Resposta

(a)

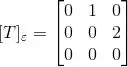
(b)

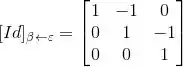
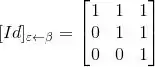
(c)

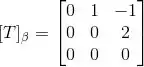
(d)

Exercícios de Livros Relacionados

Sejam E = ( u → ,v → ,w → ) uma base e F = v → - u → ,u → - w → ,u → . Mostre que F é base e calcule a tripla de coordenadas do vetor u → + 2 v → + 3 w → na base F .
Sejam E = ( e → 1 ,e → 2 ,e → 3 ) , F = ( f → 1 ,f → 2 ,f → 3 ) e G = g → 1 ,g → 2 ,g → 3 bases tais que 2 e → 1 = 3f → 1 - f → 3 g → 1 = e → 1 + e → 2 + e → 3 2 e → 2 = f → 1 + 3f → 3 g → 2 = e → 1 +
Sejam A, B, C, D matrizes de ordem n, sendo A e B semelhantes, C e D semelhantes. É verdade que A + C e B + D são semelhantes? E quanto a AC e BD?
Encontre o vetor de coordenadas de A em relação à base S = A 1 ,A 2 ,A 3 ,A 4 de M 22 . A = 2 0 - 1 3 , A 1 = - 1 1 0 0 , A 2 = 1 1 0 0 , A 3 = 0 0 1 0 eA 4 = 0 0 0 1
Considere as bases B = u 1 ,u 2 e B ' = u 1 ' ,u 2 ' de R 2 , em que u 1 = 1 0 ,u 2 = 0 1 ,u 1 ' = 2 1 ,u 2 ' = - 3 4 a) Encontre a matriz de transição de B ' para B .b) Encontre a matriz de transição