P2 de Álgebra Linear I - MAT1200 da PUCRIO - 2018.1

Seja a transformação linear que é a projeção ortogonal sobre o plano de equação

E seja a projeção afim que é a projeção ortogonal sobre um plano paralelo ao plano .

(a) Mostre que a transformação P é definida pela matriz:

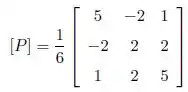
(b) Determine Im(P)

(c) Encontre uma base do espaço nulo de P

(d) Encontre, se houver, uma base de feita com vetores que sejam autovetores de P. Caso contrário, justifique.

(e) Nos itens seguintes, assuma que e determine:

e.1) A expressão para F, ou seja, determine F(x,y,z) (pode responder usando matrizes, se preferir)

e.2) A equação cartesiana do plano .

Considere o espaço vetorial das matrizes de duas linhas e duas colunas e dois subconjuntos:

(c) Determine uma base de V.

Considere o espaço vetorial das matrizes de duas linhas e duas colunas e dois subconjuntos:

(a) Mostre que U não é subespaço vetorial de

(b) Mostre que V é subespaço vetorial de .

Considere a transformação linear dada pela matriz

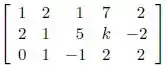
Onde k é uma constante real. Determine, se possível, o que é pedido abaixo em cada item.

Caso não seja possível, justifique.

(a) Todos os valores de k tais que

(b) Todos os valores de k tais que

(c) Todos os valores de k tais que

(d) Todos os valores de k tais que

Sejam e . Considere o conjunto .

(a) Mostre que é base do .

(b) Determine e .

(c) Determine para .

(d) A projeção (não necessariamente ortogonal) de um vetor w sobre um vetor v, na direção de um vetor u, é o vetor w’ que tem a direção de v e tal que w-w’ tem a direção de u, como a figura abaixo.

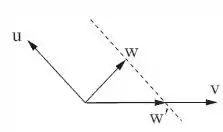
Encontre a matriz da transformação linear que é a projeção de (x,y) sobre na direção de .