Listas de Limites de Cálculo 1 da UFSC - Lista 1.5 - Continuidade Definição
Cálculo 1 - UFSC
2. Seja uma função contínua (isto é, contínua em todos os pontos do seu domínio). Sabe-se que , e . Calcule os limites de , e
Ver solução completa3. Em cada item, use as propriedades de continuidade para explicar por que a função é contínua em seu domínio.
- Considere a função cujo gráfico está representado abaixo. Determine os pontos de continuidade e descontinuidade de
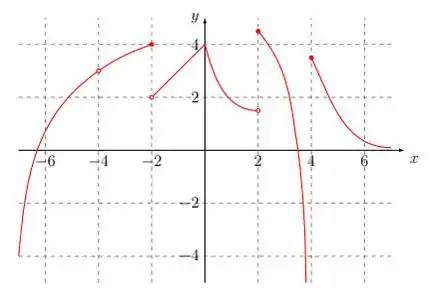
4. Use a continuidade das funções do exercício anterior para calcular os limites abaixo:
6. Considere a função
Encontre valores reais para , e tais que a função seja continua nos pontos e .
Ver solução completaC2. Classifique cada item abaixo como verdadeiro ou falso.
a) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
b) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
c) Seja . Pelo Teorema do Valor Intermediário, é possível concluir que existe ∈ [0,4] tal que .
d) A função possui, pelo menos, uma raiz real.
e) Toda função contínua possui, pelo menos, uma raiz real.
Ver solução completaC3. A função satisfaz e , isto é, e possuem sinais opostos. É possível usar o Teorema do Anulamento para concluir que possui uma raiz no intervalo (−1, 1)?
Ver solução completa