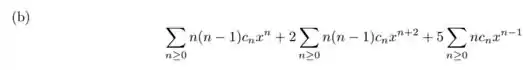Listas GMA de Equações Diferenciais da UFF - Lista 4
Equações Diferenciais - UFF
3. Prove que a série de potências é solução da equação:
Determine os três primeiros termos de uma segunda solução linearmente independente.
Ver solução completaDetermine uma cota inferior para o raio de convergência das séries obtidas como solução de
Ao redor dos pontos e .
Ver solução completa3. Prove que a série de potências é solução da equação:
OBS: No enunciado original, a série dada contém erro de digitação.
Ver solução completaUse o teorema de Frobenius para determinar soluções da seguinte equação linear homogênea ao redor dos seus pontos singulares regulares:
Ver solução completaUse o teorema de Frobenius para determinar soluções da seguinte equação linear homogênea ao redor dos seus pontos singulares regulares:
Ver solução completaUse o teorema de Frobenius para determinar soluções da seguinte equação linear homogênea ao redor dos seus pontos singulares regulares:
Ver solução completaUse o teorema de Frobenius para determinar soluções da seguinte equação linear homogênea ao redor dos seus pontos singulares regulares:
Ver solução completa