Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .
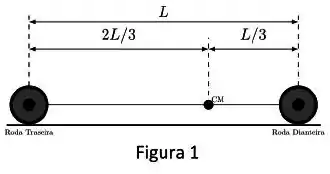
a) Sabendo que o carro completo tem massa de , calcule o valor das forças normais: da roda dianteira e na roda traseira , na situação de equilíbrio estático e repouso.
Dados:
Passo 1
Vamos começar com as forças sobre o carro.
Temos a força peso aplicada no centro de massa e as forças normais em cada roda:
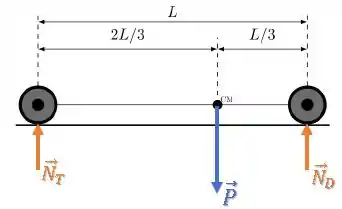
Se o carro está em equilíbrio, então:
Show!
Mas e essas forças normais?
Elas poderiam ser iguais, por exemplo?
Na verdade não...
Porque se o carro está em equilíbrio, ele também deve atender à segunda condição de equilíbrio, que é:
Então, vamos achar as forças a partir da equação de torque.
Passo 2
Devemos escolher um sentido como positivo.
Vamos escolher nessa questão o sentido ANTI-HORÁRIO como positivo.
Além disso, devemos escolher um ponto para se calcular o torque com relação a ele.
Vamos calcular a partir do centro de massa.
Começando com o torque da roda dianteira.
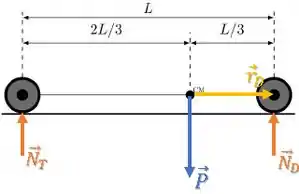
Como os vetores são perpendiculares, o torque será:
É positivo pois tenta girar o carro no sentido anti-horário.
Já o torque da roda traseira.
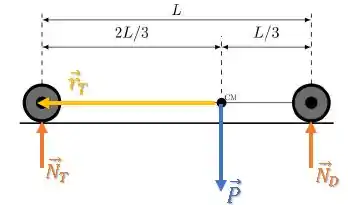
Como os vetores também são perpendiculares:
É negativo pois tenta girar o carro no sentido horário com relação ao CM.
Só resta a força peso.
Porém, como ela está aplicada no próprio eixo de rotação, ela não gera torque.
Passo 3
Voltando à equação de equilíbrio, temos:
Passo 4
Substituindo essa relação na primeira equação, temos:
Logo, temos que:
Passo 5
Substituindo os valores, temos: