Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .
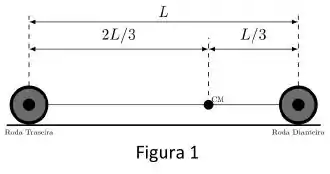
De agora em diante considere que ambas as rodas possuem raio , massa e momento de inércia ao redor do centro de massa . No item (b) existe atrito entre as rodas e o chão, e elas rolam sem deslizar.
b) A figura 2 descreve uma versão simplificada da roda dianteira em movimento. O motor realiza sobre ela um torque (para dentro da folha). A força (SI) é a força que o veículo faz sobre a roda, que é aplicada diretamente no centro de massa da roda. Calcule a aceleração angular da roda. Cuidado ao escolher a direção da força de atrito.
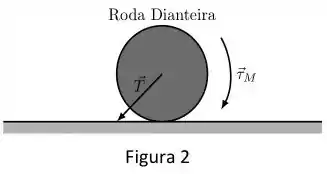
Passo 1
Vamos começar desenhando a força de atrito.
Como o torque tenta fazer a roda girar e deslizar no sentido anti-horário, a força de atrito atua contra essa tendência:
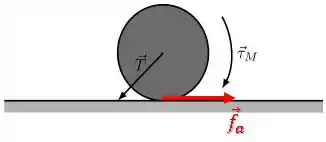
OBS:A força de atrito que é responsável por empurrar os carros para frente quando você pisa no acelerador.
Passo 2
Agora, vamos escrever a Segunda Lei de Newton na horizontal:
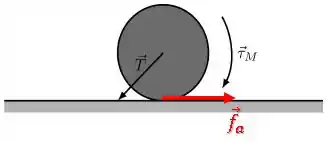
Além disso, como não há deslizamento, podemos utilizar a relação:
Então:
Passo 3
Já a Segunda Lei de Newton para rotação é:
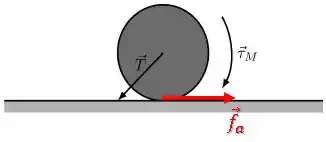
Como a força está aplicada no próprio centro de rotação da roda, seu torque é nulo:
Já o torque da força de atrito será:
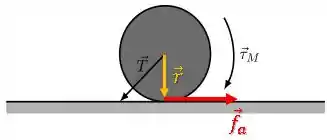
A roda gira no sentido horário, então vamos considerar o sentido de como positivo.
Assim, o torque da força de atrito é negativo, pois tenta girar a roda no sentido anti-horário:
Substituindo na Segunda Lei para rotação, temos:
Passo 4
Ficamos com um sistema assim:
As únicas duas incógnitas são e .
Queremos achar , então vamos eliminar .
Isolando na primeira equação, temos:
Substituindo isso na segunda, temos:
Colocando em evidência:
Substituindo os valores numéricos: