Dois cilindros de raios diferentes são unidos conforme a figura, sendo o raio do cilindro menor e do cilindro maior . Fios ideais, que não escorregam, são enrolados em cada um dos cilindros e na outra extremidade de cada um dos fio é pendurada uma massa . Este sistema é colocado para girar ao redor de um eixo de rotação horizontal, sem atrito. O momento de inércia deste sistema torno do eixo vale . O sistema inicialmente se encontra em repouso. Após deixarmos os pesos cair, determine a aceleração angular deste sistema utilizando as leis de Newton em termos de , a aceleração da gravidade, e de . NÃO substitua por valores numéricos.
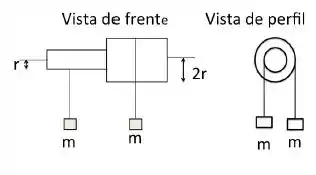
Passo 1
Para achar a aceleração angular do eixo, devemos aplicar a Segunda Lei de Newton para rotações:
Passo 2
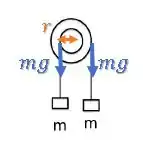
Vamos olhar para a vista de perfil.
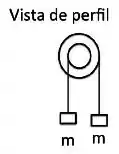
Cada bloquinho está tentando girar o eixo para um lado diferente, concorda?
Eles estão gerando uma força de tração no fio igual aos seus pesos .
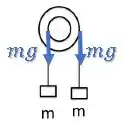
Quanto mais afastado do eixo de rotação, maior o torque. Então o eixo vai girar no sentido horário.
Mas fique tranquilo quanto ao sinal, nós queremos apenas o módulo da aceleração angular . Porém é importante colocar sinais trocados para os dois torques, já que cada um tenta girar o eixo num sentido diferente.
Passo 3
O raio do cilindro maior é :
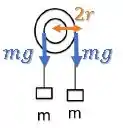
Então o torque da força mais à direita é:
Enquanto o raio do cilindro menor é .
Então o torque da força mais à esquerda é:
Considerando o sentido horário positivo, temos:
Passo 4
Substituindo o momento de inércia dado no enunciado, temos:
Assim, achamos que: