O sistema da figura ao lado é constituído por uma barra homogênea de comprimento , e massa , e um anel de raio e massa . Este anel está fixo em uma das extremidades da barra e a outra extremidade pode girar em torno de um eixo de rotação horizontal. Inicialmente o sistema se encontra em repouso, com a barra e o anel em um plano horizontal. O objeto então é liberado e pode girar livremente, sem atrito, em torno do eixo (a figura mostra o objeto na parte mais baixa de sua trajetória)
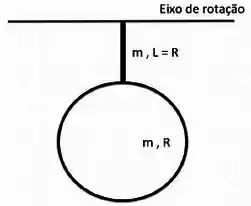
a) Calcule o momento de inércia do objeto em relação ao eixo descrito (dados: momento de inércia da barra em torno de seu centro de massa , momento de inércia do anel com eixo de rotação ao redor de um diâmetro ).
b) Calcule a velocidade angular do objeto ao passar na parte mais baixa da trajetória (Lembre-se, quando a barra se encontra na horizontal o objeto esta em repouso).
Passo 1
O momento de inércia dessa coisa aí, vai ser a soma do momento de inércia da barra com o do anel:
Então é só usar as fórmulas de momento de inércia que ele nos deu no enunciado??
Infelizmente não...
Isso porque o momento de inércia é sempre calculado com relação a um eixo de rotação. As fórmulas de momento estão com relação a um eixo que não é o eixo de rotação do problema.
Então, vamos usar o teorema dos eixos paralelos:
Passo 2
Vamos começar com a barra.
O momento de inércia dado na fórmula é com relação a um eixo passando pelo seu centro de massa:
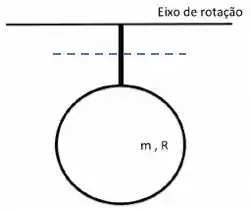
Então, para achar o com relação ao eixo de rotação, basta achar a distância entre os eixos.
Nesse caso ela será igual a metade do comprimento da barra:
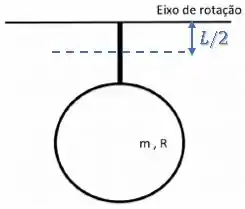
Como o comprimento da barra é igual a , temos:
Passo 3
Vamos ao anel.
O momento de inércia dado na fórmula é com relação a um eixo passando pela direção de um diâmetro, ou seja, pode ser uma eixo assim:
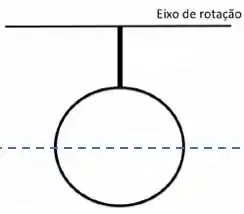
Como escolhemos um eixo que paralelo ao eixo de rotação e que passa pelo centro de massa do anel, podemos usar o teorema.
A distância entre os eixos será o comprimento da barra mais o raio do anel .
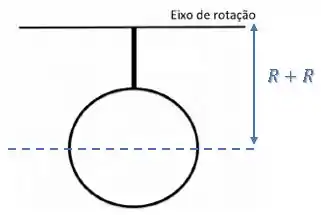
Passo 4
O momento de inércia da coisa toda é:
Passo 5
Agora, queremos saber a velocidade angular do objeto quando ele passa na parte mais baixa de sua trajetória.
Como não há atrito, temos uma conservação da energia mecânica.
Inicialmente o corpo está em repouso com uma energia potencial gravitacional e no ponto mais baixo de sua trajetória, há apenas energia cinética de rotação .
Passo 6
A energia potencial gravitacional é dada com relação ao centro de gravidade do objeto.
Então, vamos achar esse ponto...
O centro de gravidade da barra (uniforme) está em seu meio e o do anel (uniforme) também está em seu centro:
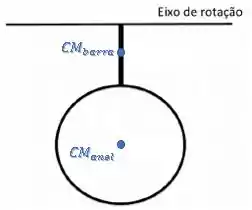
Agora, podemos pensar em cada um deles como uma partícula nesses pontos e fazer uma média ponderada das suas posições:
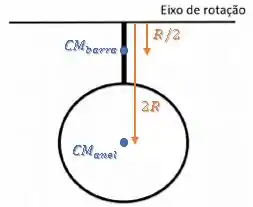
Então, o centro de gravidade do objeto será:
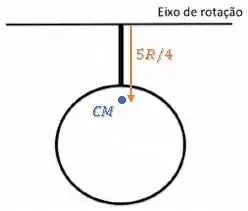
Então, se o objeto descer de um plano horizontal até ficar na vertical, ele descerá uma altura igual a essa distância do CM ao eixo de rotação:
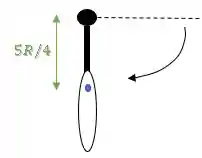
Então, a energia potencial gravitacional inicial é:
Passo 7
Voltando à conservação de energia:
Substiituindo o momento de inércia do objeto que achamos no item (a):
Assim, achamos que a velocidade angular no ponto mais baixo é:
Resposta
(a)
(b)