Um disco (1), de massa , raio e momento de inércia ao redor de seu centro de massa , desliza em um plano horizontal, sem atrito, com velocidade e velocidade angular (veja a figura), onde o eixo se situa para fora da folha. Em , o disco 1 colide com um disco 2 idêntico a ele, de modo que os dois saem grudados em suas extremidades.
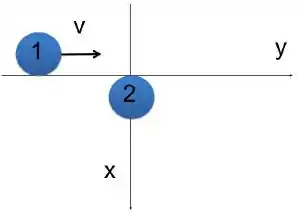
a) Dentre as grandezas seguintes: energia cinética, momento linear e momento angular, diga quais se conservam, e quais não se conservam. Justifique.
b) Calcule a velocidade do centro de massa do sistema formado pelos dois discos antes e depois da colisão.
c) Descreva o movimento do sistema formado pelos dois discos grudados após a colisão, e calcule a velocidade angular final dos discos após a colisão.
Passo 1
Na letra (a), vamos responder cada uma delas separadamente.
Energia Cinética: Não se conserva, pois a colisão é inelástica.
Numa colisão elástica há conservação da energia cinética, entretanto, na inelástica não há.
Momento Linear: Se conserva, pois não há ação de forças externas.
Como o plano é horizontal, as forças peso e normal se concelam, ou seja, a força resultante externa é nula.
Além disso, as forças entre os dois discos são forças internas (mesma intensidade e sentidos opostos) logo elas também se cancelam.
Assim, o momento linear se conserva:
Momento Angular: Se conserva, pois não há torques externos no sistema.
A mesma ideia que usamos para o momento linear na translação, usamos para o momento angular na rotação.
As forças externas como peso e normal não geram torque nos discos, portanto, não há torque externo, então:
Passo 2
Na letra (b), queremos a velocidade do CM antes e depois da colisão.
Vamos primeiro conservar o momento linear para achar a velocidade dos discos após a colisão.
Inicialmente, apenas o disco (1) se movia com uma velocidade .
Após a colisão, os discos andam juntos com uma velocidade .
Queremos a velocidade do centro de massa, certo?
Bom, mas como os discos andam juntos após a colisão, o centro de massa estará exatamente na mesma velocidade que eles. Então:
E ainda podemos usar mais uma malandragem...
Como não há forças externas atuando no sistema, a velocidade do centro de massa se conserva. Então, a velocidade do centro de massa antes da colisão é a mesma que após a colisão:
Passo 3
Na letra (c), vamos primeiro descrever o movimento após a colisão.
Após a colisão, os dois discos saem colados e apresentam tanto um movimento de translação quanto de rotação em torno do centro de massa do sistema.
A velocidade de translação deles é .
Vamos calcular agora a velocidade angular deles.
Passo 4
Para isso, vamos usar a conservação do momento angular:
Passo 5
O momento de inércia inicial é o do disco (1) com relação a um eixo passando pelo seu centro de massa:
Já na situação após a colisão, temos que o sistema gira em torno do centro de massa:
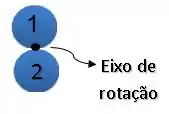
Então, precisamos aplicar o teorema dos eixos paralelos para descobrir o momento de inércia de um disco com um eixo perpendicular passando pela sua extremidade.
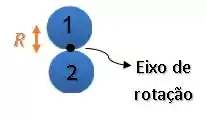
Então, o momento de inércia do conjunto de dois discos será:
Passo 6
Voltando na conservação de momento angular, temos:
E o vetor será no mesmo sentido da velocidade angular inicial:
Resposta
(a)
Energia Cinética: Não se conserva, pois a colisão é inelástica.
Momento Linear: Se conserva, pois não há ação de forças externas.
Momento Angular: Se conserva, pois não há torques externos no sistema.
(b)
(c)
O conjunto dos dois discos translada com e rotaciona em torno do centro de massa (ponto que une os dois discos) com velocidade angular .