Um disco isolado de forças externas possui raio R e massa m e é feito de um material capaz de se reorganizar internamente. Inicialmente o material está homogeneamente espalhado por todo o disco e possui velocidade angular em torno do centro de massa. Num outro instante, toda a massa se aglomera na borda.

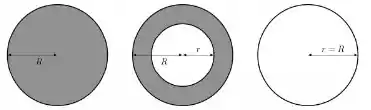
b) Encontre a velocidade angular final em função da velocidade angular inicial, justificando seu raciocínio com base em princípios físicos.

Bem parecida com a questão anterior, né? Como não tem nenhum torque externo agindo no sistema de novo, o momento angularse conserva! Nesse caso, o sistema inicialmente tem o momento de inércia de um disco homogêneo, e depois de muito tempo seu momento de inércia será o de um anel homogêneo, os dois de raio R. Então temos que:

SHOW DIMAI!