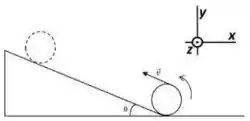
Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.

c) Calcule o trabalho total sobre a bola necessário para fazê-la parar.

d) Calcule a distância D que a bola percorre ao longo do plano inclinado até parar.

c) Na letra c a gente só precisa lembrar do teorema trabalho e energia cinétcia! Então

Mas como queremos parar a bolinha, , então

E foi dada que a velocidade no topo (5m/s) e que no rolamento suave a Velocidade do Centro de Massa vale a metade disso, então:

E também sabemos que , então substituindo tudo isso na equação, ficamos com:

Tranquilassoooo! Vamo pra próxima!