Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Uma partícula pontual de massa m = 1,0kg se move sobre uma superfície sem atrito com velocidade constante v = 3,0m/s. Nessa mesma superfície existe um disco homogêneo de raio R =0,50 m e massa M =10 kg que gira com velocidade angular desconhecida (inclusive seu sentido) ao redor de um eixo fixo preso a seu centro de massa. Ao alcançar o disco, a partícula se agarra a ele formando um sistema composto.
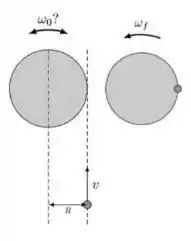
- Se a velocidade angular final do sistema, com relação ao centro de massa do disco é = 2,0rad/s no sentido anti-horário, calcule a velocidade angular Inicial do disco e indique seu sentido (horário ou anti-horário).
Passo 1
Como não tem nenhum torque externo agindo no sistema, o momento angular antes da colisão será o mesmo que depois da colisão, lembra? Vamo escolher o centro como ponto de referência para calcular os momentos angulares. O momento angular da partícula ANTES da colisão é:
E do disco:
Depois da colisão o sistema gira ao redor do centro do disco com uma nova velocidade angular. O momento de inércia desse sistema depois da colisão vai ser a soma dos momentos de inércia do disco com o da partícula, né? Ou seja:
O momento angular total depois da colisão é:
Agora, finalmente podemos aplicar a conservação dos momentos angulares! Então:
No sentido Anti-Horário, que também se conservou! Fechamoooo!