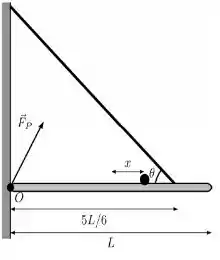
Uma haste homogênea de comprimento L e massa M está presa por uma das extremidades a uma parede pelo ponto O. A haste é mantida na horizontal por uma corda que se prende a uma distância igual a 5L/6 e faz um angulo θ = 36,8° com a haste. Sobre a haste existe ainda uma massa pontual m posicionada à distância x do centro de massa da haste. A força da parede sobre a haste está representada na figura como

1. Calcule a expressão literal para o momento de inércia I do sistema [haste + massa pontual] com relação a um eixo perpendicular à figura que atravessa o ponto O.

Nos próximos itens, adote: M = 100 kg, m = 12,0 kg e L = 1,20 m.

2. Sabendo que a tensão T na corda não pode exceder 1160 N, encontre o valor máximo de x para que a corda não se rompa.
3. Na situação do item (b), encontre o módulo da força que a parede realiza na haste.
4. Suponha que a massa m se encontra a um valor x = 0,25m e que a corda se rompeu. No instante que a corda se rompe, calcule a aceleração angular α do sistema.

Podemos usar o ponto de referência O para calcular o torque resultante do sistema, que deve ser nulo porque o corpo tá em equilíbrio. A vantagem de escolher esse ponto é que o torque da força da parede é nulo com relação a O, sacou? Como estamos no limite do rompimento da corda, a tensão na corda T é a tensão máxima permitida T=1160 N. Tomando também os torques no sentido anti-horário como positivos temos que:

Calculando cada torque com os dados que temos, ficamos com:

Como temos essa força na diagonal, podemos decompor ela no eixo x e no eixo y, e a gente sabe que o somatório das forças em todas as direções deve ser nulo, então:

Agora é só calcular o módulo da força!

Fechouuu! Próxima!

Agora nosso torque resultante será diferente de 0, e noxxo x=0,25m e teremos que:

E usando o resultado da letra a pra calcularmos o momento de Inércia, temos:

Jogando na fórmula do equilíbrio dos torques, temos:

Showww! Acabmos! :D