Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.
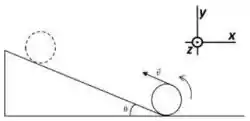
- Faça um diagrama de corpo livre que represente a bola num ponto qualquer do plano inclinado.
- Calcule o módulo do torque resultante () sobre a bola e forneça sua direção e sentido em termos dos vetores unitários de acordo com o sistema de coordenadas da figura.
Passo 1
- Fala aí! Vamo nessa?
- Pra gente calcular o Torque resultante, a gente sabe que:
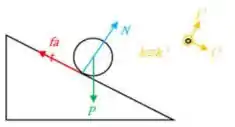
Lembra que como a bola ta subindo, ela tende a deslizar pra baixo, então nossa força de atrito tem esse sentido! Fechou? :D
Passo 2
E como o corpo que a gente tá tratando é uma bolinha (aproximadamente uma esfera oca) nosso centro de massa vai ser assim:
Mas vamos pensar agora... Quem é essa força resultante? A força Normal e a força Peso nesse caso não vão realizar nenhum torque, porque elas passam exatamente no centro de massa da bolinha! Então, nosso torque vai ser realizado pela força de atrito!
E sendo , temos:
Show, mas a gente ainda precisa descobrir essa eceleração do Centro de Massa aí...
E pra gente fazer isso, é só usarmos o equilíbrio de forças! Como a força Py se anula com a Normal, temos:
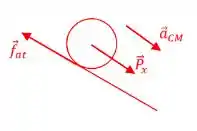
Então . Então...
Como , e
Porém, como esse torque faz a bola girar num sentido horário, temos que
Toppppíssimo! Vamo lá!
Resposta
a)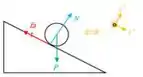 
b)