P2 de Física 1 da UFRJ - 2012.2
Física 1 - UFRJ
Um pai de massa brinca com seu filho de massa na superfície horizontal de um lago congelado, onde o atrito pode ser desprezado; considere . Cada um segura uma das extremidades de uma corda leve e comprida. Eles devem puxar a corda para conseguir pegar uma bola, colocada na metade da distância entre os dois. Qual a afirmação é verdadeira quando ambos puxam a corda?
- O resultado dependerá do esforço que cada um fará.
- O pai, alcançará a bola primeiro.
- O filho alcançará a bola primeiro, qualquer que seja seu esforço.
- Os dois sempre alcançarão a bola ao mesmo tempo.
- Nenhuma das afirmações anteriores.
Um trenó de massa move-se horizontalmente com velocidade constante em um lago congelado. Ao passar por baixo de um viaduto, cai sobre ele verticalmente, um pacote de massa ficando preso a ele. O atrito entre as superfícies do lago e o trenó pode ser desprezado. Ao comparar-se, o momento linear, a velocidade, e a energia cinética do sistema trenó-pacote após o pacote cair sobre o trenó, é correto afirmar que:
- aumenta, diminui e aumenta;
- aumenta, permanece constante e aumenta;
- Diminui, diminui e diminui;
- permanece constante, permanece constante e permanece constante;
- permanece constante, diminui e diminui;
Uma esfera de massa , raio e momento de inércia , em relação ao eixo que passa pelo seu centro de massa, desce um plano inclinado (ver figura), rolando sem deslizar. A esfera parte do repouso e desce até o final do plano inclinado (ponto ), situado a uma altura em relação ao solo. Neste instante, ela tem velocidade angular , e entra em queda livre. Afirma-se que: Imediatamente antes de tocar o solo, a velocidade angular da esfera é . Imediatamente antes de tocar o solo, a velocidade angular da esfera continua com valor . O momento angular da esfera mantém-se perpendicular ao plano do movimento. Ao longo da queda livre, a energia cinética de rotação da esfera permanece constante. Qual(ais) da(s) afirmação(ões) acima está(ão) incorreta(s)?
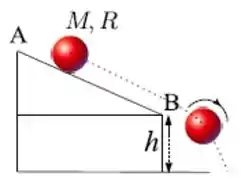
- Somente a .
- Somente a .
- e .
- e .
- e .
Uma bola desloca-se com velocidade constante e colide elasticamente na lateral de uma mesa, segundo o ângulo definido entre a direção de seu movimento e a lateral da mesa e é claro que ; como mostra a figura. O processo de colisão dura um tempo . Na figura estão indicadas setas numeradas. A opção correta para representar a força média que atua na bola durante a colisão é:
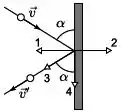
- ;
- ;
- ;
- ;
- nenhuma das respostas anteriores;
Um bloco deslocando-se com momento linear , colide com um bloco de momento linear , onde é constante. Suponha que não há força externa. Após a colisão o centro de massa do sistema segue, de acordo com o sistema de coordenadas ortogonais e os respectivos vetories unitários , e :
- na direção e sentido negativo;
- na direção e sentido negativo;
- na direção e sentido positivo;
- na direção e sentido positivo;
- em uma direção formando um ângulo com os eixos e .
Um menino, de massa , encontra-se na extremidade esqueda de um barco de comprimento e massa , distribuída homogeneamente. Inicialmente o conjunto, barco e menino, move-se para a direita com velocidade constante , em relação a um referencial inercial colocado na margem do lago. Num dado instante o menino move-se para a extremidade direita do barco, onde permanece. Nesta situação o conjunto move-se com velocidade constante em relação ao mesmo referencial inercial. Desprezando-se o atrito entre o barco e a água, pode-se afirmar, ao fim do processo, que:
- .
- .
- .
- Não se pode determinar , pois não se conhece a força exercida pelo menino sobre o barco.
- Não se pode determinar , pois não se conhece a velocidade inicial do centro de massa do sistema barco-menino.
Um caracol de massa encontra-se inicialmente em repouso na extremidade, ponto , de uma barra rígida e homogênea de comprimento (conforme a figura), que gira com velocidade angular em torno de um eixo fixo que passa pelo ponto , perpendicularmente a barra horizontal. Em um certo instante, o caracol desloca-se até a extremidade oposta da barra, ponto , onde permanece. Nesta situação a barra gira com velocidade angular . Sendo , o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto e o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto , das opções abaixo, a correta é
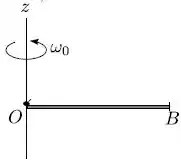
- ;
- ;
- ;
- ;
- ;
Um disco de massa rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal, mantendo-se sempre alinhado verticalmente. Nos diagramas abaixo, , , e , aquele que presenta corretamente os vetores velocidade (indicados por setas) dos pontos e , da periferia do disco e o seu centro, em relação a um observador parado na Terra é
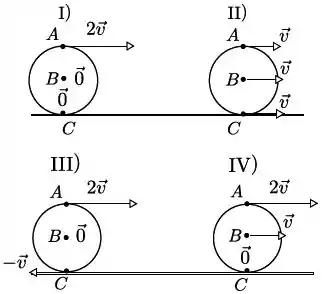
- nenhum deles
Um disco uniforme é montado em um eixo horizontal de massa desprezível, em torno do qual pode girar livremente, como mostra o diagrama. O momento de inércia do disco em relação ao eixo é . O disco está inicialmente girando com velocidade angular ; vide figura. O disco é movimento horizontalmente para esquerda até que sua face entre em contato com um disco idêntico, que está inicialmente em repouso. Depois de um pequeno intervalo de tempo, os dois discos acoplam-se e passa a girar juntos com uma velocidade angular final . Em relação às grandezas: velocidade angular final, energia cinética de rotação e momento angular do sistema, pode-se afirmar que ao final do processo de acoplamento:
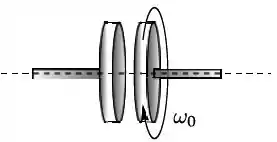
- , não é conservada, não é conservado;
- , é conservada, não é conservado;
- , é conservada, não é conservado;
- , não é conservada, é conservado;
- , é conservada, é conservado;
Uma partícula de massa move-se inicialmente com velocidade de módulo ao longo de uma trajetória retilínea que forma um ângulo de com o eixo , como mostra a figura. Ela colide com uma segunda partícula que tem duas vezes sua massa, isto é , que está movendo-se ao longo da direção e sentido positivo com velocidade de módulo três vezes maior que , ou seja: . Depois da colisão, a primeira partícula move-se ao longo da direção e sentido negativo, enquanto que a segunda partícula continua a mover-se ao longo do eixo e sentido positivo, com uma velocidade escalar reduzida. Considere que não atuam forças externas sobre as partículas. Se na solução de algum item abaixo for usada alguma lei de conservação, justifique-a.
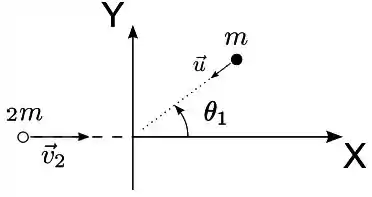
- Determine o vetor momento linear total inicial para este sistema de duas partículas;
- Calcule os módulos das velocidades de ambas as partículas depois da colisão em função dos dados do problema;
- Determine o vetor velocidade do centro de massa do sistema antes e depois da colisão.
Dados: ; .
Ver solução completaUma barra delgada homogênea e uniforme, de massa e comprimento , é articulada num pino , que passa por uma de suas extremidades, e pode girar sem atrito num plano vertical. Liberada a partir do repouso na posição horizontal, a barra sofre uma colisão elástica com um pêndulo ao passar pela posição vertical, como representa a massa de dimensões desprezíveis presa à extremidade da haste. O pêndulo também pode oscilar em torno do pino, sem atrito, no mesmo plano vertical que a barra. Sabe-se que o pêndulo encontrava-se em repouso antes da colisão com a barra, e que o momento de inércia da barra em relação ao eixo perpenducular ao plano vertical e que passa pelo pino é
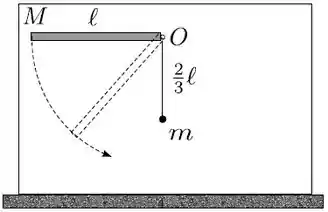
- Determine a velocidade angular da barra, , imediatamente antes da colisão com o pêndulo.
- Quais das seguintes grandezas: o momento linear e o momento angular em relação a são conservadas na colisão? Justifique a sua resposta.
- Determine a velocidade angular da barra, , imediatamente após a colisão.
- Determine o valor da razão para que a barra permaneça em repouso depois da colisão.
Uma chapa metálica quadrada de lado , homogênea e de massa encontra-se em repouso sobre um plano horizontal , sem atrito, com o seu centro de massa localizado na origem . Num dado instante aplicam-se as forças e em dois vértices da chapa como mostra a figura. A opção que corresponde ao torque resultante em relação ao ponto , imediatamente após as forças serem aplicadas é:
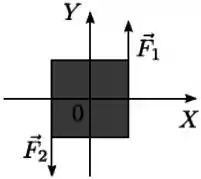
- ;
- ;
- ;
- ;