Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 841234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283858687888990919293949596979899100

Enunciado

Rotação

Um disco de massa M rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal, mantendo-se sempre alinhado verticalmente. Nos diagramas abaixo, I ) , I I ) , I I I ) e I V ) , aquele que presenta corretamente os vetores velocidade (indicados por setas) dos pontos A e C , da periferia do disco e B o seu centro, em relação a um observador parado na Terra é

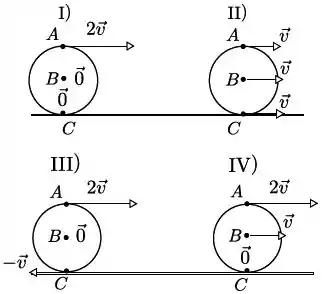
  1. nenhum deles
  2. I
  3. I I
  4. I I I
  5. I V

Passo 1

Numa rotação a velocidade de um ponto é

v = R ⋅ ω

Onde R é a distância do centro de rotação até aquele ponto.

Já vimos que quando alguma coisa rola sem deslizar pelo chão o ponto de contato com o chão tem velocidade igual a zero, porque ele é o ponto de rotação.

Então

v C = 0

Passo 2

Se ele roda com velocidade ω e o cilindro tem raio R , vamos ter

v B = R ⋅ ω = R ω

E

v A = 2 R ⋅ ω = 2 R ω

Dessa forma a velocidade em A é o dobro da em B .

O diagrama que mostra isso é o I V

Resposta

Letra E

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida