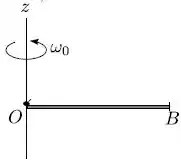
Um caracol de massa encontra-se inicialmente em repouso na extremidade, ponto , de uma barra rígida e homogênea de comprimento (conforme a figura), que gira com velocidade angular em torno de um eixo fixo que passa pelo ponto , perpendicularmente a barra horizontal. Em um certo instante, o caracol desloca-se até a extremidade oposta da barra, ponto , onde permanece. Nesta situação a barra gira com velocidade angular . Sendo , o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto e o momento de inércia do sistema com relação ao eixo quando o caracol está no ponto , das opções abaixo, a correta é
- ;
- ;
- ;
- ;
- ;
Passo 1
Como não temos ação de torques externos o momento angular se conserva. Nesse caso vamos calculá-lo com a seguinte fórmula
Então quando o caracol está no ponto
Onde
Ao chegar no ponto o momento de inercia do sistema mudou, já que agora o caracol tem uma certa distância do centro
Dessa forma
Passo 2
Igualando
Como
A velocidade angular deve diminuir
Resposta
Letra A