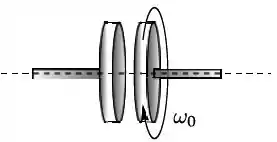
Um disco uniforme é montado em um eixo horizontal de massa desprezível, em torno do qual pode girar livremente, como mostra o diagrama. O momento de inércia do disco em relação ao eixo é . O disco está inicialmente girando com velocidade angular ; vide figura. O disco é movimento horizontalmente para esquerda até que sua face entre em contato com um disco idêntico, que está inicialmente em repouso. Depois de um pequeno intervalo de tempo, os dois discos acoplam-se e passa a girar juntos com uma velocidade angular final . Em relação às grandezas: velocidade angular final, energia cinética de rotação e momento angular do sistema, pode-se afirmar que ao final do processo de acoplamento:
- , não é conservada, não é conservado;
- , é conservada, não é conservado;
- , é conservada, não é conservado;
- , não é conservada, é conservado;
- , é conservada, é conservado;
Passo 1
Como não temos torques externos o momento angular do sistema se conserva
Vamos ter
E
Igualando vamos ter
Passo 2
Já vimos que o momento angular é conservado vamos agora calcular a energia cinética inicial e a final, que neste caso é apenas de rotação
E
Como
Vamos ter
Então a energia cinética não se conserva
Resposta
Letra D