Dinâmica de Rotação
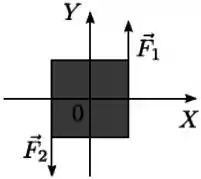
Uma chapa metálica quadrada de lado , homogênea e de massa encontra-se em repouso sobre um plano horizontal , sem atrito, com o seu centro de massa localizado na origem . Num dado instante aplicam-se as forças e em dois vértices da chapa como mostra a figura. A opção que corresponde ao torque resultante em relação ao ponto , imediatamente após as forças serem aplicadas é:
- ;
- ;
- ;
- ;
Passo 1
Repara que as forças estão inclinadas em relação ao ponto . O braço de cada uma delas vai ser metade do lado do quadrado, como vimos na teoria.
Porque as forças fazem a chapa girar no sentido anti-horário.
Passo 2
O torque resultante vai ser
Sabemos que a placa girará, nesse caso, no sentido anti-horário e, portanto, usando a regra da mão direita, temos:
Resposta
Letra B
Exercícios de Livros Relacionados
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2