Rotação
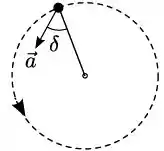
Uma partícula de massa está girando em torno de um eixo (perpendicular a página) com movimento de rotação uniformemente variando com aceleração , como mostra a figura; vista de cima. O raio de trajetória é e o vetor aceleração da partícula tem a sua direção formando um ângulo com a direção radial. Num dado instante ela tem velocidade angular e aceleração angular . Pode-se afirmar que:
- ;
- ;
- ;
- ;
- ;
Passo 1
Essa aceleração faz um ângulo com o eixo no desenho.
Vamos decompor essa aceleração, para que vamos fazer isso? Para achar a aceleração centrípeta e a aceleração tangencial. Usando a regra do “COlado/SEparado”
Passo 2
Lembrando que
E nesse caso
A aceleração centrípeta fica
Passo 3
E temos também que
Passo 4
Vamos ter então
Dividindo a segunda equação pela primeira
Então
Resposta
Letra B
Exercícios de Livros Relacionados
Em uma rasteira de judô, você tira o apoio do pé esquerdo do adversário e, ao mesmo tempo, puxa seu quimono para o lado sem apoio. Em consequência, o lutador gira em torno do pé direito e cai no tatam
Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/s2, qual é o momento de inércia da roda?
Duas forças agem sobre um corpo. Quais das seguintes afirmações estão corretas?(a) O corpo está em equilíbrio se as forças são iguais em módulo e contrárias em direção.(b) O corpo está em equilíbrio s
Uma polia, com um momento de inércia de 1,0 X 10- 3 kg · m2 em relação ao eixo e um raio de 10 cm, é submetida a uma força aplicada tangencialmente à borda. O módulo da força varia no tempo de acordo
Na figura abaixo, um cilindro com uma massa de 2,0k g pode girar em torno do eixo central, que passa pelo ponto O. As forças mostradas têm os seguintes módulos: F → 1 = 6,0N , F → 2 = 4,0N , F → 3 = 2